Weekly Commentary: Million Dollar Smile

Crypto-twitter is abuzz following a high-profile bet on massive dollar devaluation and its implications on BTC’s spot price.

We take a look at the extreme probabilities implied by the million-dollar price tag attached to the wager by decomposing it into two options and comparing their prices to those quoted by the wider market.

Balajis’ Bet

Figure 1: Twitter user @balajis’ tweet accepting @jdcmedlock’s bet that the US will not enter hyperinflation.

Crypto-twitter is abuzz following a high-profile bet on massive dollar devaluation and its implications on BTC’s spot price. Twitter users @balajis and @jdcmedlock have committed 1M USDC and 1 BTC respectively to a third party escrow account. If BTC trades higher than $1M after 90 days, @balajis will receive $1M USDC and 1 BTC. If BTC trades lower than that strike price on that date, @jdcmedlock will receive the USDC and BTC instead in a winner-takes-all arrangement.

Decomposing the Bet

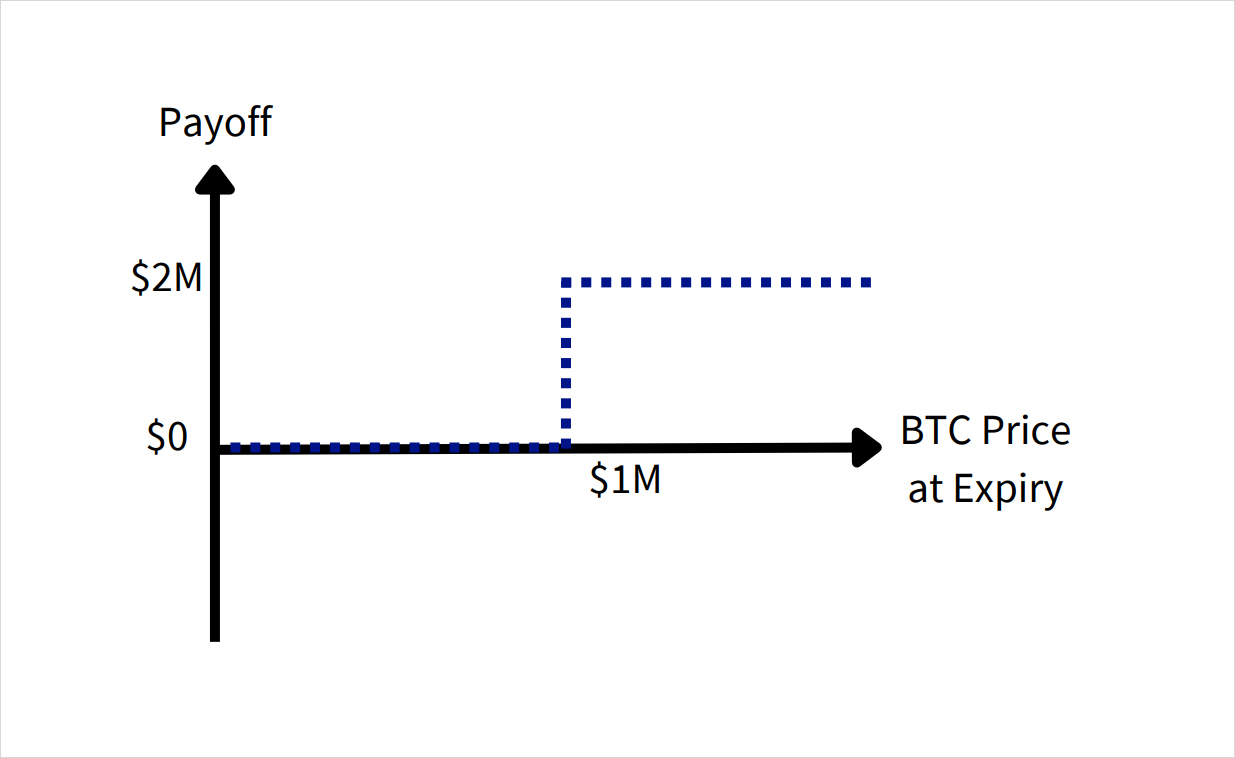
Working from @balajis’ perspective, we can decompose this bet into two more familiar options: a digital call option with a $1M strike that pays $2M, and a vanilla call option with a strike also at $1M.

A digital call option pays out a fixed rate only if the underlying is above the strike price (in our case if the price of BTC is above $1M). Ignoring the initial cost of $1M, we get the following payoff diagram:

The vanilla call option is more familar, paying the difference between the spot price at expiry and the strike price if that is postive, and zero otherwise:

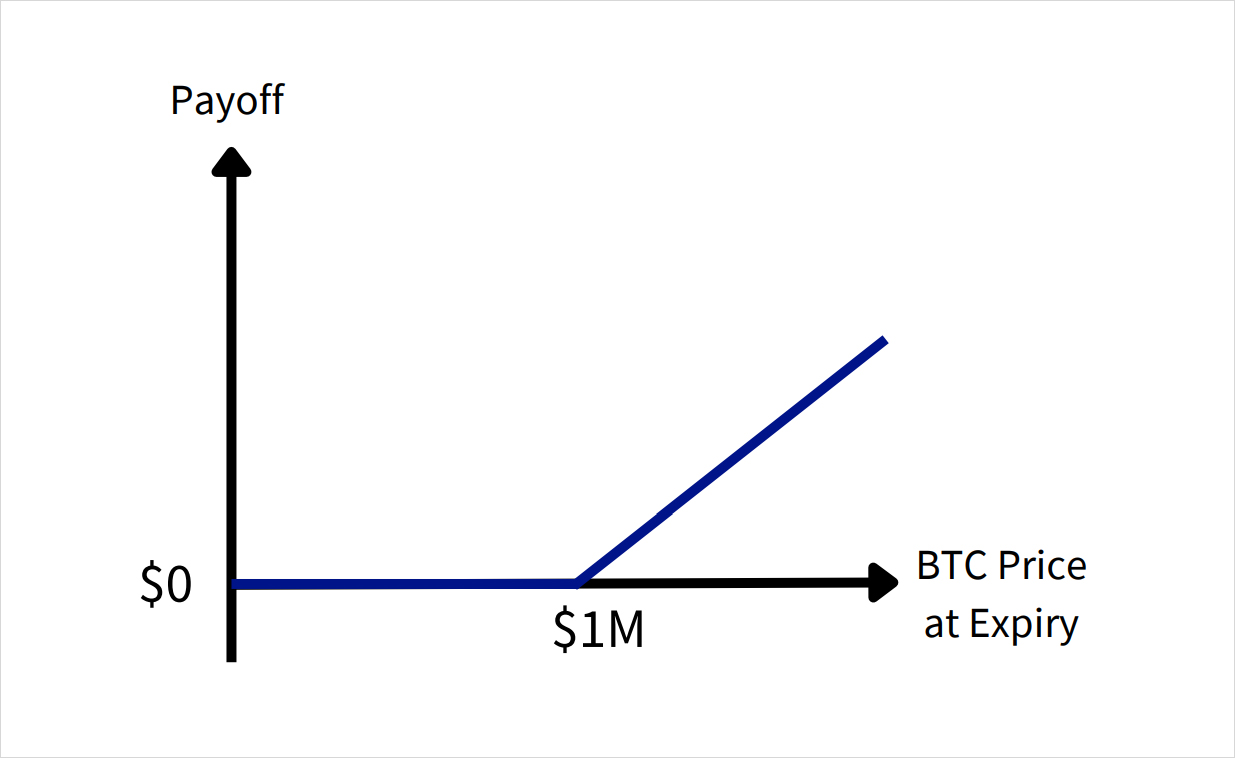
If we consider the initial cost of $1M for this portfolio, we can replicate @balajis’ final PnL using the vanilla and digital calls described above:

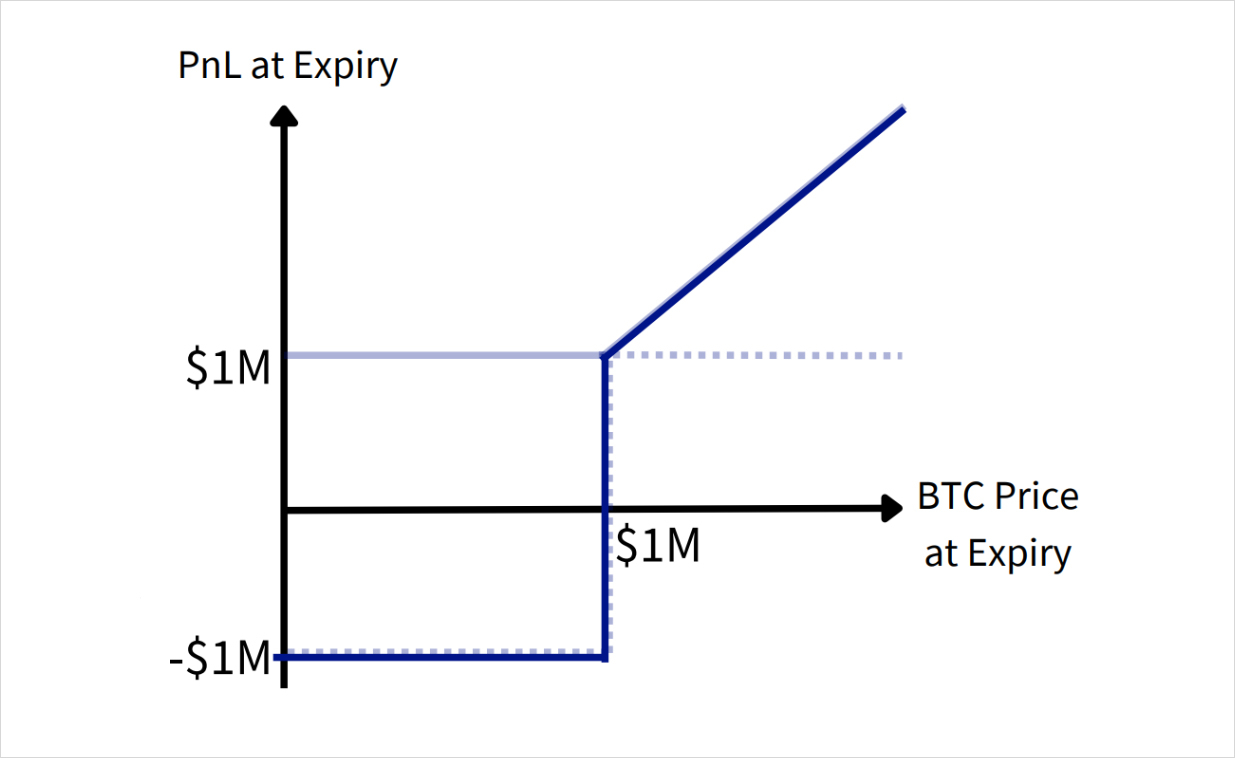
If BTC trades above $1M, @balajis receives a PnL of 1 BTC, now worth in excess of $1M. If instead BTC trades below $1M, @balajis loses $1M. Note that the payoff for @jdcmedlock is symmetric to @balajis’, and that we have now included the cost of the bet to @balajis, $1M.

Market Pricing

Using the mark price of a $1M strike option listed on ByBit’s USDC options exchange, we can easily find the market price for a vanilla call, expiring on the 30th June, an expiry close to 90 days away.

Figure 2: The bid and ask prices of a vanilla call with a strike of $1M and expiry of 30th June 23, as quoted on ByBit. Source: ByBit.com

As the orderbook on ByBit’s exchange* shows, the mark price of @balajis’ call is just $0.42. This reflects the market’s belief that the probability of the option expiring in-the-money is exceptionally low. Despite this, the option has been traded three times so far by users emulating the bet, exchanging hands for as high as $15. The volatility implied by the market price of the just the vanilla call ($0.42) is 162.54%, whose corresponding distribution implies a probability of exercise of just 0.000072%.

For @balajis’ $1M price tag to make sense, noting that the full bet is decomposed not only into the vanilla call priced above, but also includes a digital call paying out $2M if BTC exceeds the strike, the probability of BTC trading above the $1M strike price must be much higher.

This bet is clearly not intended to be taken at face value, as @balajis stated rationale is to “ring the fire alarm” on the impending devaluation of the dollar.

Figure 3: Twitter user @balajis’ tweet explaining the rationale behind his bet.

Whilst the market is not pricing as extremely as @balajis’ bet implies, we have seen a strong move towards OTM calls at a 3M strike as the market expresses a similar bullish view on BTC. This is perhaps linked to the narrative that Bitcoin is a hedge against the traditional financial system, one that has reemerged in recent weeks following the troubles faced by several banks in the US.

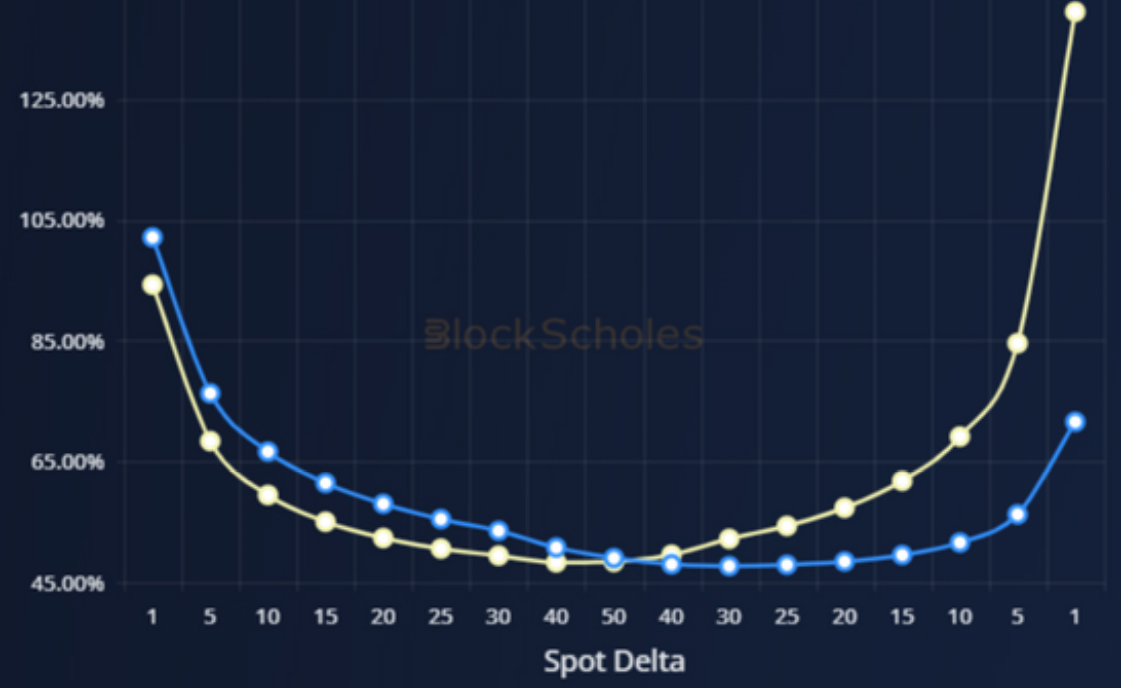
Figure 4: BTC volatility smiles at a 1M tenor as traded on ByBit at 21st Mar 23 (yellow) and 10th Mar 23 (blue) snapshots. Source: Block Scholes

Note that the ByBit market data used to price these options is at an extreme strike, with a total quantity of 0.18 BTC quoted by all bids in the orderbook. The pricing used in this analysis is based on the volatility smile calibrated to that level of orderbook liquidity.