Introduction to Option Greeks

The Greeks can sometimes be intimidating for new option traders, as there is nothing comparable in futures or spot trading, however, they are simpler than they may first appear. Greeks are simply a measure of an option’s price sensitivity to changes in various external variables.

Much like option prices obtained from a mathematical model (for example the Black Scholes formula), the Greeks are also theoretical values obtained from a calculation. They change over the life of the option contract depending on each of the inputs to the model that generates them.

Delta – Underlying price sensitivity

An option’s delta is one of the most important Greeks, as it measures by how much the option price is expected to move based on a $1 increase in the underlying asset price.

• Value of Delta always varies between -1 and 1
• Call options have a delta between 0 and 1
• Put options have a delta between -1 and 0

Example:

A delta of 0.50 means the price of the option is expected to increase by $0.50 for a $1 increase in the underlying asset price.

A delta of -0.40 means the price of an option is expected to decrease by $0.40 for a $1 increase in the underlying asset.

The delta of call options is always positive, and the delta of put options is always negative. As the price of the underlying asset price increases, you would expect call option prices to rise and put option prices to fall.

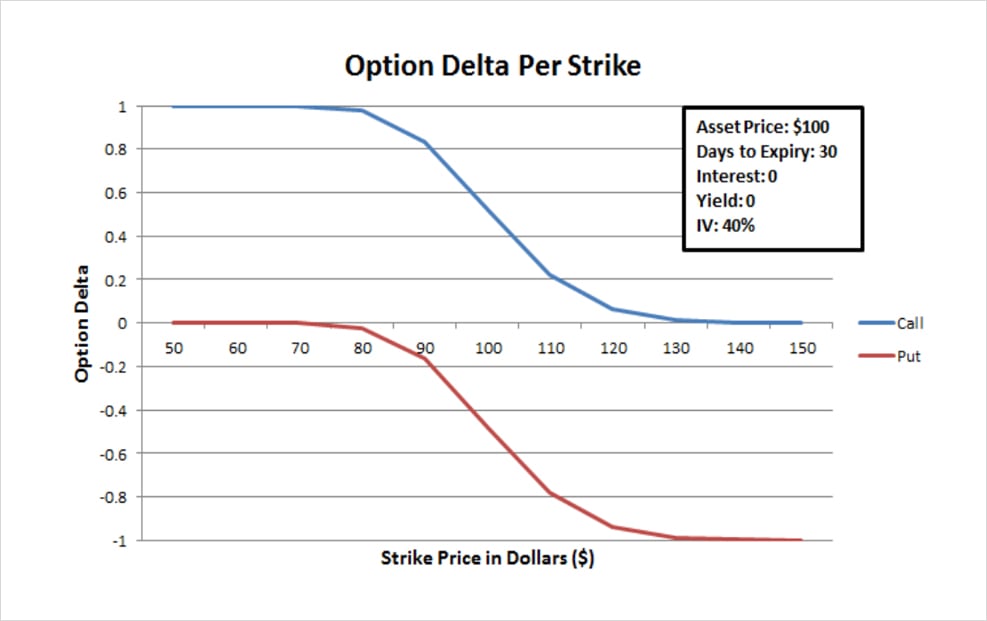
This graph shows an asset with a current price of $100, 30 days to expiry and implied volatility of 40%.

Deep in the money calls will have delta approaching 1, meaning that they mimic a long position of the underlying asset. At the money calls will have a delta of roughly 0.5. And far out of the money calls will have delta approaching 0.

Deep in the money puts will have delta approaching -1, meaning that they mimic a short position of the underlying asset. At the money puts will have a delta of roughly -0.5. And far out of the money puts will have delta approaching 0.

Gamma – Rate of change of delta

An option’s gamma is a measure of how much the delta is expected to change based on a $1 increase in the underlying asset price. The higher an option’s gamma the more the option delta will change if the underlying price moves by $1.

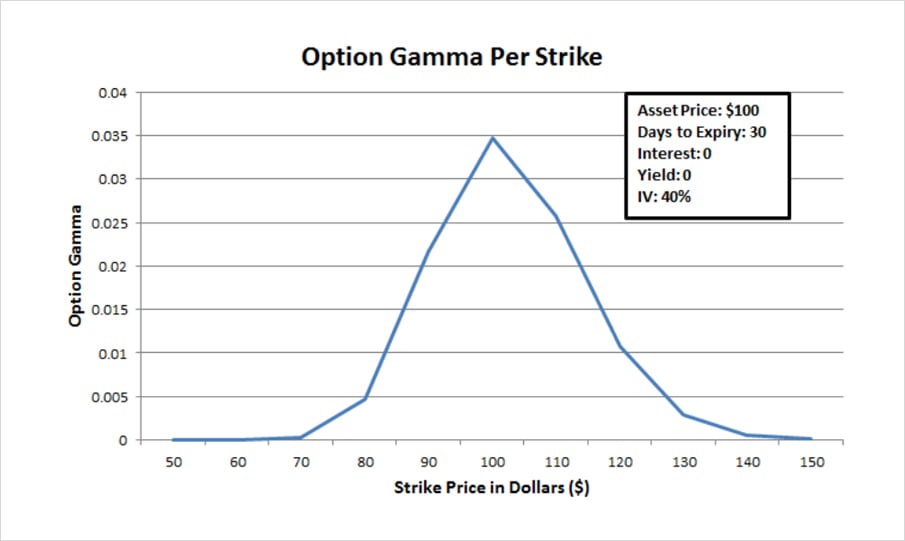
Much like the extrinsic value of an option, gamma is the highest for at the money options and decreases, as the current price moves away from the strike price.

You can see this in the next graph. It is the same asset as in the first example, with a current price of $100, 30 days to expiry and implied volatility of 40%. The at the money strike at $100 has the highest gamma, decreasing in both directions for strike prices further away from the current price.

Theta – Time decay

An option’s theta is a measure of how the option price is expected to change with the passage of time, also known as time decay. Specifically how much the option price is expected to change in one day.

As with gamma, it is the at the money options that are affected the most by theta as shown in the graph below.

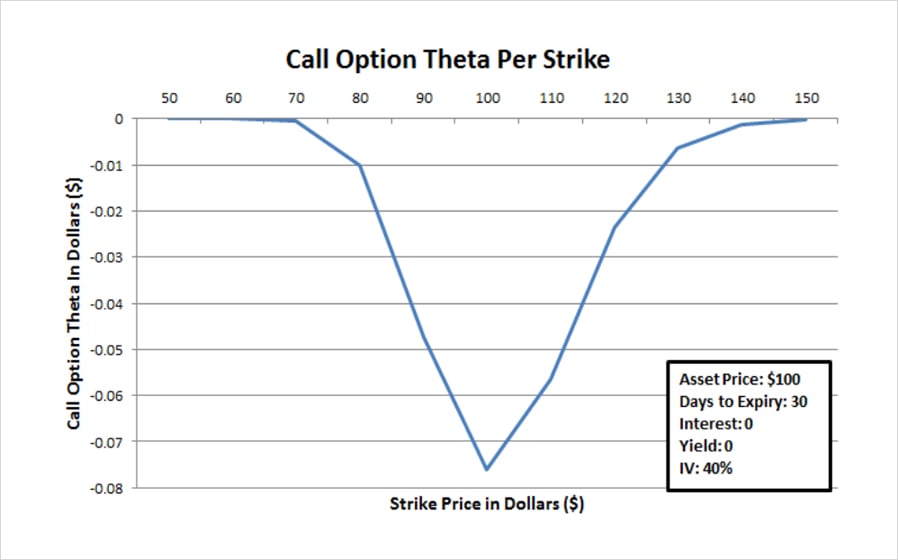
Theta is always negative for call and put option buyers, as all other things being equal, an option will lose extrinsic value with every day that passes until eventually at expiry it has no extrinsic value.

At the money strikes of course have the most extrinsic value, and so have the most value to lose to time decay.

The more negative the theta, the more value the option is expected to lose over the next day.

Example:

An option with theta of -0.04 is expected to lose $0.04 of value over the next day, all other things being equal.

An option with theta of -2 is expected to lose $2 of value over the next day, all other things being equal.

Vega – Volatility sensitivity

An option’s vega is a measure of how much the option price will change for a 1% change in implied volatility.

Example:

With a vega of 2, we can expect a 1% increase in implied volatility to cause the option price to increase by $2.

Vega is also is the highest for at the money options, as shown in the graph below:

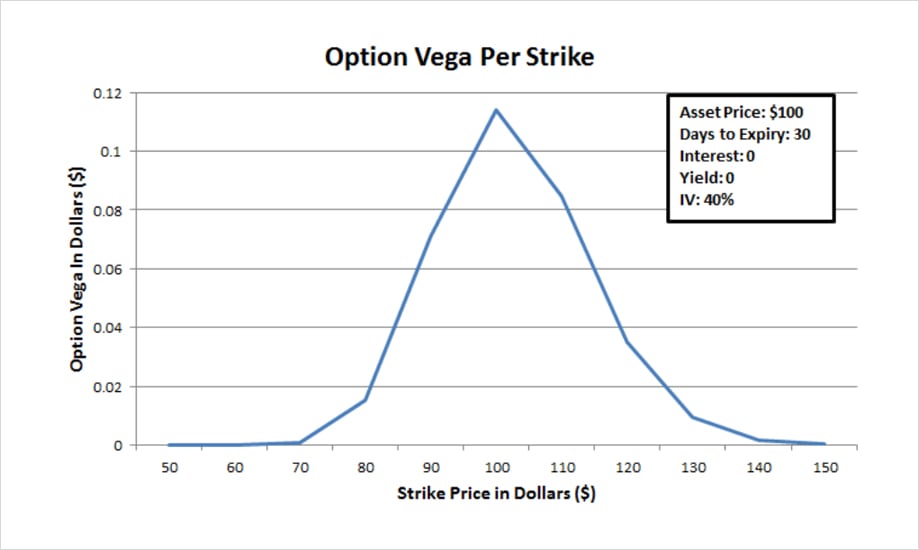
The higher an option’s vega the more the option price will go up for a 1% increase in implied volatility (and vice versa).

Where to find the greeks on Deribit?

On the options page you can find a ‘Delta’ column. You can enable/disable this column using the checkbox at the top. This column shows the delta for every option, one column for calls and one for puts. If you hover over the delta value for any option, the gamma, theta and vega will also be displayed as seen in the photo below.

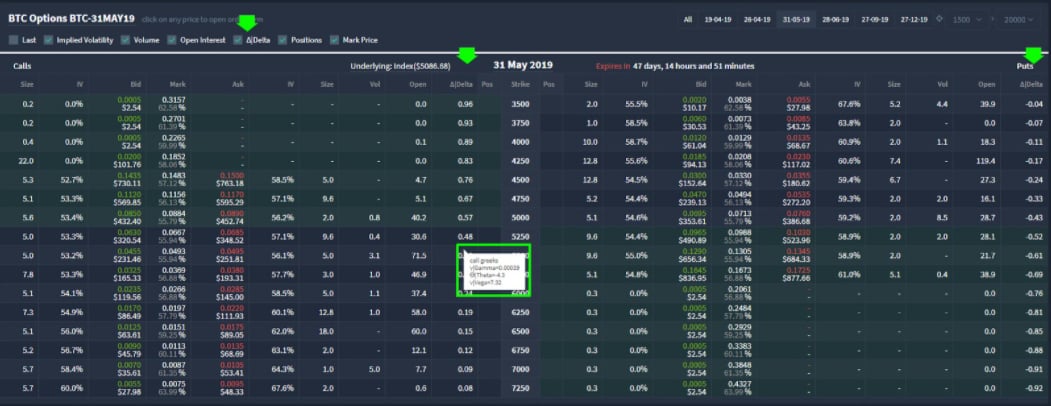
You’ve now got a basic overview of the main option greeks and where to find their values on Deribit.

Summary of all Greeks:

• Delta – Underlying price sensitivity
• Gamma – Rate of change of delta
• Theta – Time decay
• Vega – Volatility sensitivity