
In both crypto and traditional options markets, you may have heard market participants discuss the level of skew exhibited. This is a key measure of market sentiment and flows because it encapsulates what people are willing to pay to acquire an asymmetric payout on either the upward or downward direction of the market.
Today, we explore what this word means from an intuitive point of view, and hopefully this article enables you to better follow such discussions.
A 36K Dec Call
Let’s take the example of a deep out-of-the-money BTC/USD call option, the 36,000 strike call expiring 25th December 2020 on Deribit. It was featured recently in a popular tweet that pointed out traders could make 100x+ return on investment if BTC went to 50,000+ by the end of the year.
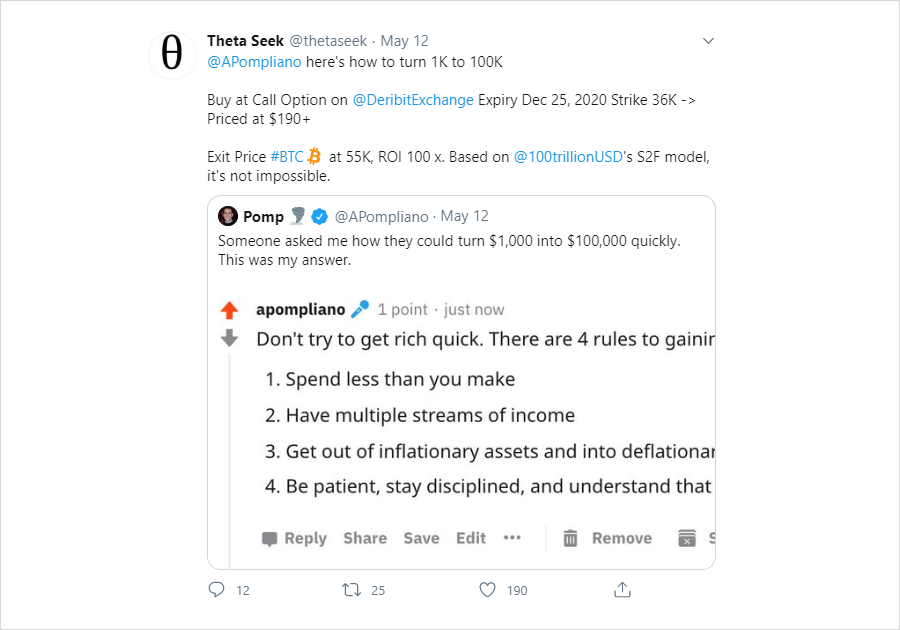
Source: Twitter
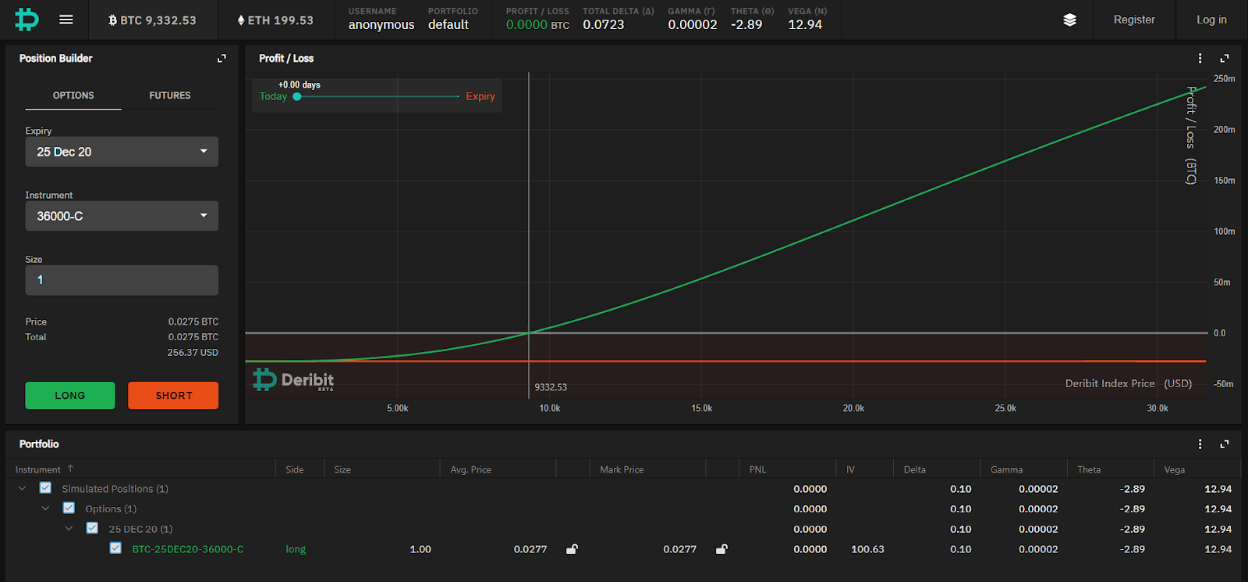
In buying this call, we obtain the right but not the obligation to buy BTC at 36,000 on 25th Dec. We can visualize the risks and profit & loss associated with this option, as well as any other combination of options, swaps, and futures, via the Position Builder on Deribit.
If BTC ended at 55,000 on 25th Dec, then the call would allow us to buy it at 36,000 and pocket the 19,000 difference. You don’t need to have the capital to “spend” 55,000, the Deribit system would simply credit you the $19,000 profit in BTC.
Naturally, we note that today, when BTC is still 9,300, this call has no intrinsic value because it is not in-the-money. In other words, nobody would pay anything for this option if it were expiring today because the strike price (36000) is far above the current price (9300). They can just buy BTC on the open market instead of acquiring this call.
So why are people willing to pay $190 for this option despite the fact that it is intrinsically worthless? Why does the price of this call go higher today based on spot BTC going from 9k to 10k, despite the fact that both 9k and 10k are very far from 36k?
In a word, time.
Time Value
The 36K call’s entire value comes from its time value, the market’s perception of how much the asymmetric proposition of being able to buy BTC at 36K at a time far in the future might be worth given the underlying volatility of BTC. The more volatile BTC is, the more likely extreme outcomes become.
In other words, in a volatile world, the unlikely becomes more likely. You wouldn’t want to own a 6-month call option struck at 400% of the current value of a house, a car, or even most stocks, but you may be happy to own it on BTC given its high realized volatility. If you had owned the equivalent call in 2017, let’s say a $4k call when BTC was $1k and before it went to $20k, you would have become a very happy investor indeed.
Abstracting Implied Volatility from Prices
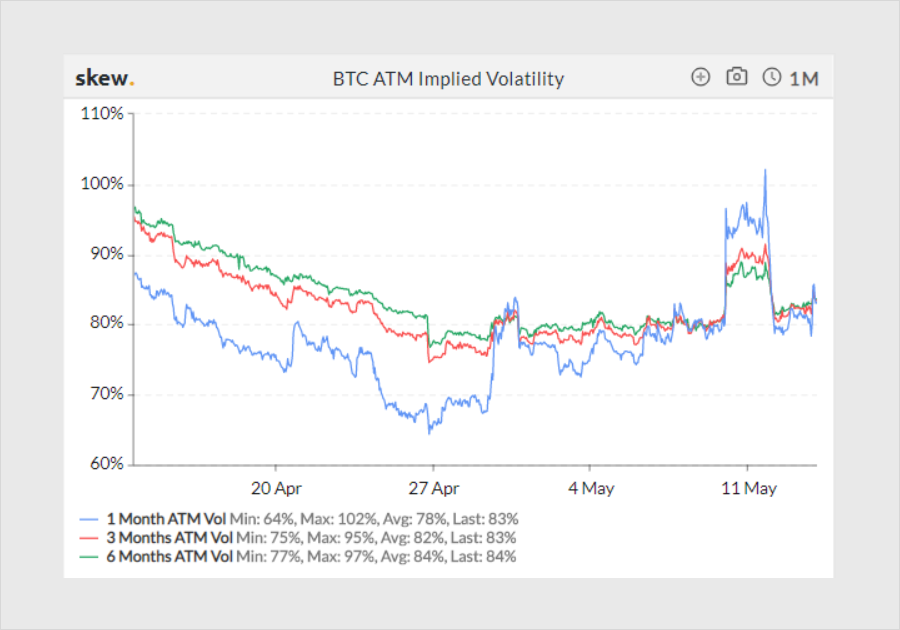
Source: Skew
Here we see a chart of 1month, 3month, and 6month implied volatilities over the last month.
When the market discusses implied volatility going up or “vols going up,” it is important to remember that this is an abstraction, a mental construct, for time value. What I mean by this is that actual prices are observed while implied volatilities are derived–most commonly from the Black Scholes model. The model is not a prescription on what to do, but rather a framework employed to make options prices more human-readable. It gives traders a common language to discuss the relative pricing of options with different expiries and strikes.
So when we say vols are going up, it means the market sees aggressive buyers of calls and puts and that time values are increasing commensurately. The higher prices of these options imply that the market expects higher volatility. Conversely, when we say vols are going down, it means sellers of calls and puts have come in and believe that the market is pricing in too much future movement. They are wagering that the time value premium they collect will be sufficiently high relative to the risk they are taking.
Below, we see that after the popular tweet, traders invested aggressively in the 36K call and pushed its price (and implied volatility) significantly higher. In the below chart, we see that it sticks out in particular against the price of similar call options with lower strikes such as the 24K call.
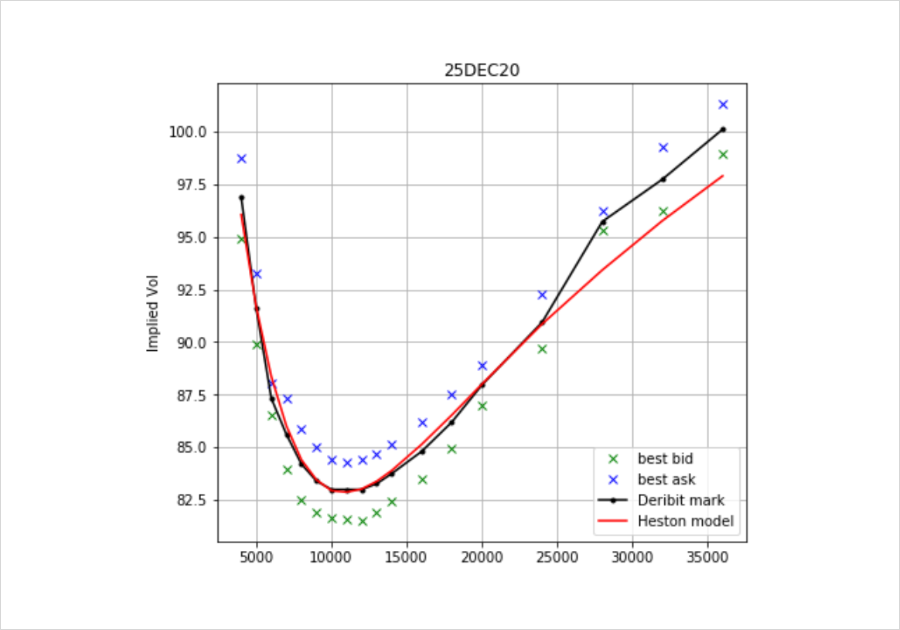
Source: Twitter
The tweet also suggests that traders could consider doing a call spread, to buy the 24K and sell the 36K call, to profit from this phenomenon. Indeed, very often in relative value options trading, the best opportunities occur when market participants buy or sell a specific flavor of option. Arbitrageurs and other sharp traders will facilitate that flow and then offset their risk in related but not entirely identical contracts. So if too many participants crowd into the 36K call and there are no natural sellers, then even still other traders would sell them these calls and then buy the 24K calls to hedge.
Skew
Equipped with this knowledge, we can come back to skew and realize we are inventing a language to assess the relative price of calls versus puts.
The most common measure of skew is the 25d. This means we compare the implied volatility of the out-of-the-money call with 25% delta against the out-of-the-money put with 25% delta. Delta can be understood as the probability that the option will expire in-the-money.; a 5K 1-week Call when price is at $9.3k would have near-100% delta, while a 36K 1-week call would have near-0% delta. This is because it is a near-certainty that the 5K call would remain ITM while the 36K would remain OTM given usual volatilities.
An example of a 25d call would be the 12K 26th Jun; it is decently out-of-the-money but still within reach given the time to maturity. Of course, at any given time the 25d call for 26th Jun depends on the spot price of BTC itself; if BTC were to rally substantially, the 12K call would no longer be the 25d call–its probability that it ends ITM would have increased and the 13K or 14K would be more closer to 25d. Any arbitrage strike can become 25d given the requisite moves in spot and vol.
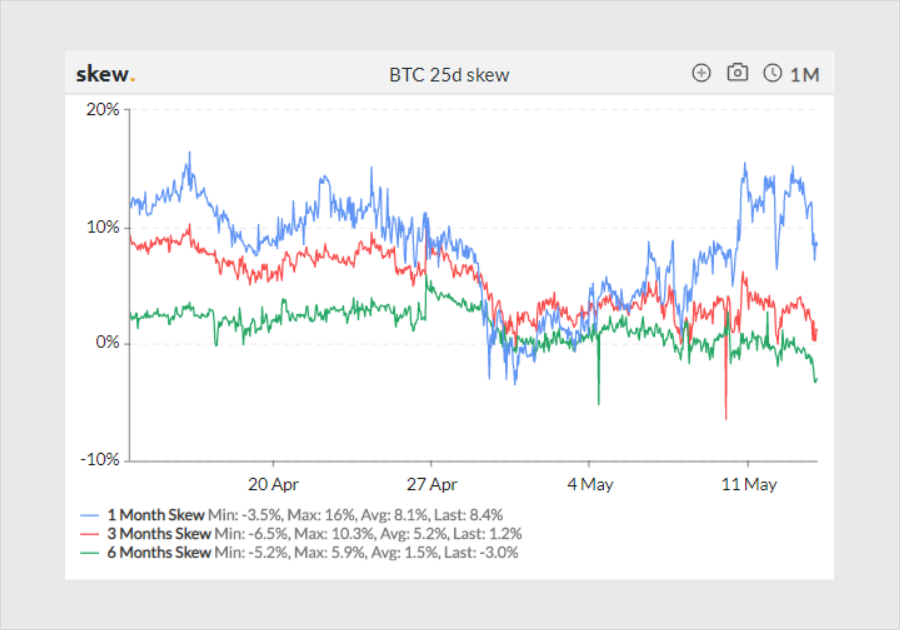
Here we see a chart of 1M, 3M, and 6M 25d skew over the past month. The y-axis measures the difference in implied volatility between the 25d call and the 25d put of the same expiry.
Positive skew means the market wants to pay to own upside payouts relative to downside payouts.
A market in positive skew is “pricing in optimism;” natural longs may be refraining from selling calls on their existing coins and speculators may be buying calls to have leveraged participation to upside. Conversely, a market in negative skew is pricing in pessimism. Coin-holders or miners may be buying puts to hedge downside risk.
Conclusion
In equity index markets, volatility tends to exhibit a natural smirk. Because investors structurally own a large amount of equities, they enter the options markets to buy protection against falling prices. They generally want the most liquid macro hedge, such as SPY puts, so they will bid these up to defend against a deterioration in their overall portfolios. Conversely, in single stock vol markets, volatility is often a smile. Imagine the day before a big earnings announcement; you surely would be happy to pay more for both calls and puts as you expect a more bimodal distribution of outcomes.
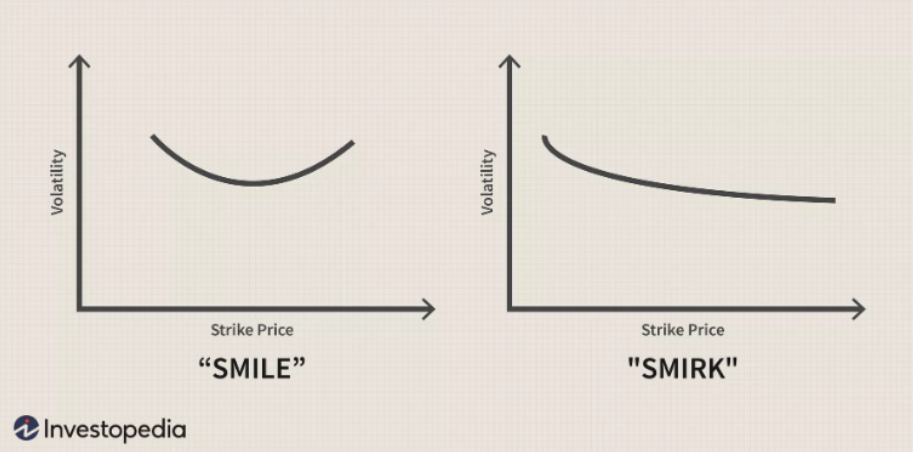
Given the parabolic advance that Bitcoin has exhibited over the past decade, positive skew would seem logical in normal market conditions. By buying OTM calls, traders can benefit from historically high upside volatility. Recently, with the popularity of covered call strategies–that is, coin-holders selling calls against their existing holdings, skew has become significantly less positive and actually goes negative frequently. Depending on your view, this represents an opportunity to harvest. If you’re bullish, you can own OTM calls instead of spot when skew is cheap and own spot instead of calls when skew is expensive. If you’re bearish, you can do similarly with puts. In essence, by understanding skew you can use it to your advantage by expressing your view against the implied probabilities of the options market.
Useful References:
Understand how multiple positions and the changing value of BTC or ETH could affect your portfolio.
Practice trading with “paper” and avoid risking real capital.
AUTHOR(S)
