A cash secured put is a strategy that involves selling a put option, while also holding a cash balance. The cash balance held is large enough to purchase the underlying at the strike price of the sold put option, and is therefore securing the traders ability to honour their obligation to purchase the underlying from the put buyer.
Of course the options on Deribit are cash settled, so if the put expires ITM, the put seller would not actually purchase the underlying from the put buyer, but instead only pay the difference between the strike price and the underlying price at expiration. However, the principle is the same in that the cash is securing the put seller’s ability to pay out any possible difference that could occur, including the possibility of the underlying price going close to zero.
Much like the covered call that we covered in the previous lecture, a cash secured put is a relatively simple position that still has the ability to cause a little confusion for some traders who are not used to trading inverse contracts, or using the base currency as collateral. Specifically, some traders mistakenly believe that because their account balance is stored in the base currency rather than the quote currency, that it’s not possible to execute a cash secured put on the inverse contracts on Deribit. Thankfully this is not accurate, and as we will show a bit later, with only a small additional step, it is indeed possible to execute a cash secured put on the inverse contracts on Deribit.
As a put is sold, and the only other part of the position is cash, the cash secured put is a bullish strategy which gives us a positive delta. The strategy is constructed by:
-Selling a put option
-Holding enough cash in the account such that there is enough to purchase the underlying at the strike price. The strike price of the put option sold is typically OTM, meaning the strike price is below the underlying price when the position is open.
Holding cash involves no risk or reward related to the underlying price of the asset, so the payoff chart is identical to that of the sold put. This gives us a payoff chart that looks like this at expiry:
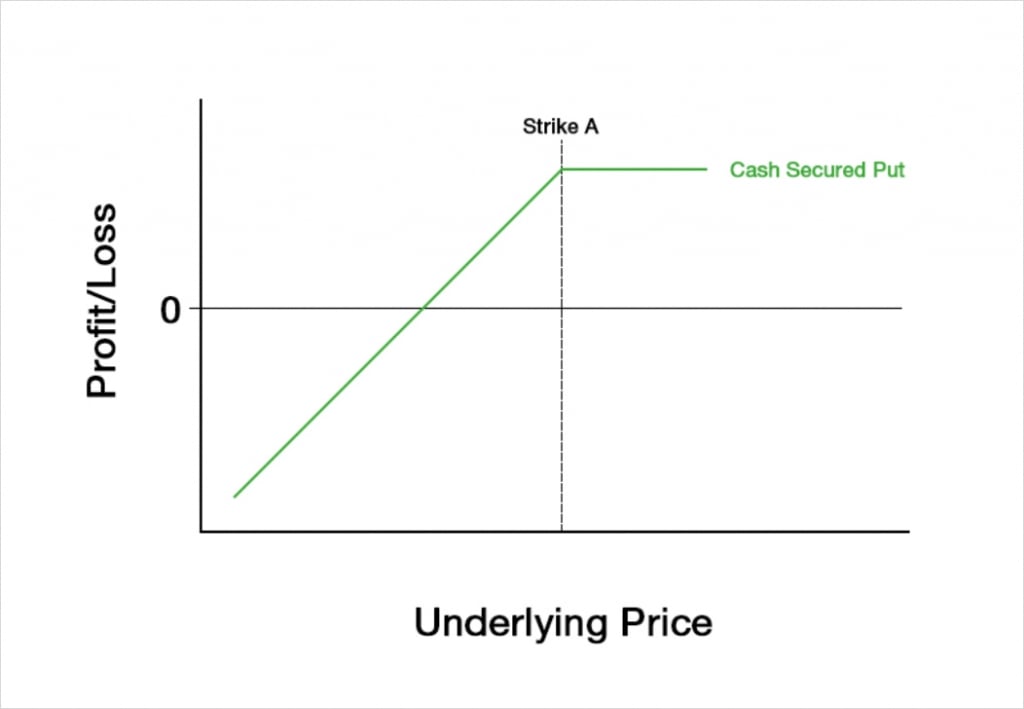
You may have noticed that this payoff chart looks very similar to that of the covered call that we discussed in the previous lecture. As we said in that lecture, if we purchase the underlying asset and simultaneously sell a call option at strike A, this is equivalent to simply selling a put option at strike A.
Assuming the put that is sold is OTM, the maximum profit is limited to the credit received. The maximum profit occurs when the underlying price at expiry is above the strike price.
The risk is to the downside as we are committed to purchasing the underlying at the strike price no matter how low the underlying price is at expiry.
The Greeks
A cash secured put is a combination of an option position, which has all the usual Greeks that we have been covering so far in the course, and a cash position, which has no Greek values at all. So the Greeks for the cash secured put will be the same as the Greeks for shorting the put. Due to this, we won’t spend too long on the Greeks for this strategy.
To analyse how the Greeks behave we will need to assign some figures to each of the Black Scholes parameters. For today’s example of a cash secured put we will assume the following parameters:
Underlying price: $100
Time to expiry: 50 days
Interest rate: 0
Implied volatility: 60%
Strike A: $90
This means that we will sell 1 put option with a strike price of $90, and also have $90 in our trading account so that we can afford to purchase the underlying for $90 if we are obliged to at expiry.
Profit and loss
With these parameters the cash secured put will initially give us a credit of about $4.32. The payoff chart looks like this.
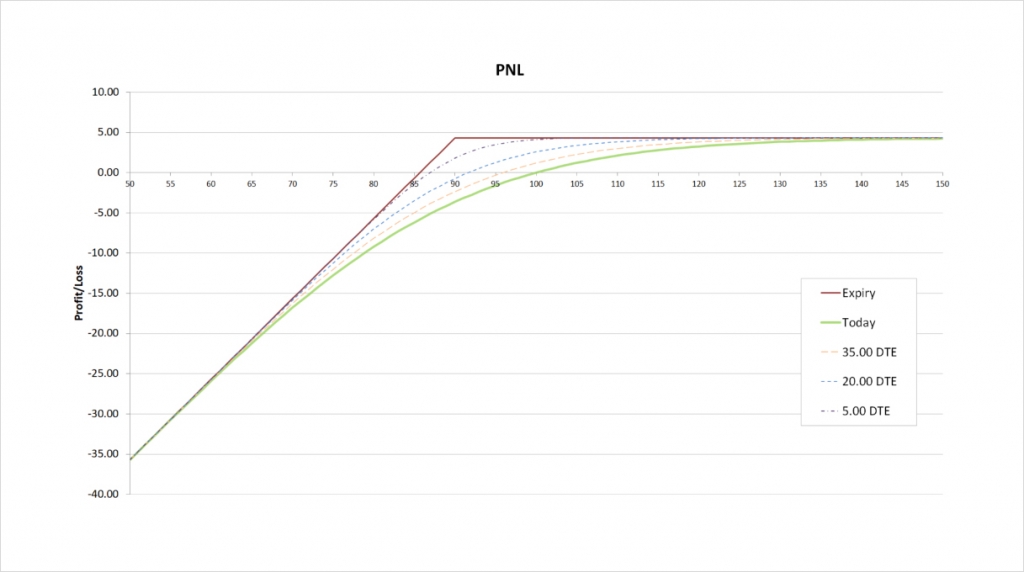
As the put sold was OTM when the position was opened, the maximum profit is capped at the premium collected, which is $4.32. The maximum profit occurs when the underlying price is above the strike price of $90 at expiry.
The maximum loss is only capped by the underlying price reaching zero. Just like the covered call, a cash secured put has (almost) unlimited risk. If the price of the underlying decreases significantly, the losses from the sold put can far outweigh the credit received for selling the put.
The breakeven price can be calculated by subtracting the credit received for selling the call from the strike price of $100. This gives us:
$90 – $4.32 = $85.68
Delta
As a cash secured put is a bullish strategy that benefits from increases in the underlying price, the total delta will be positive. We are short the $90 put which always gives us a positive delta between 0 and 1. We also hold cash, but this does not affect the delta at all, so the delta for our cash secured put will always be somewhere between 0 and 1.
This chart shows the delta of the cash secured put, with the x axis being the underlying price. The extra lines also show how the delta will evolve as time passes.
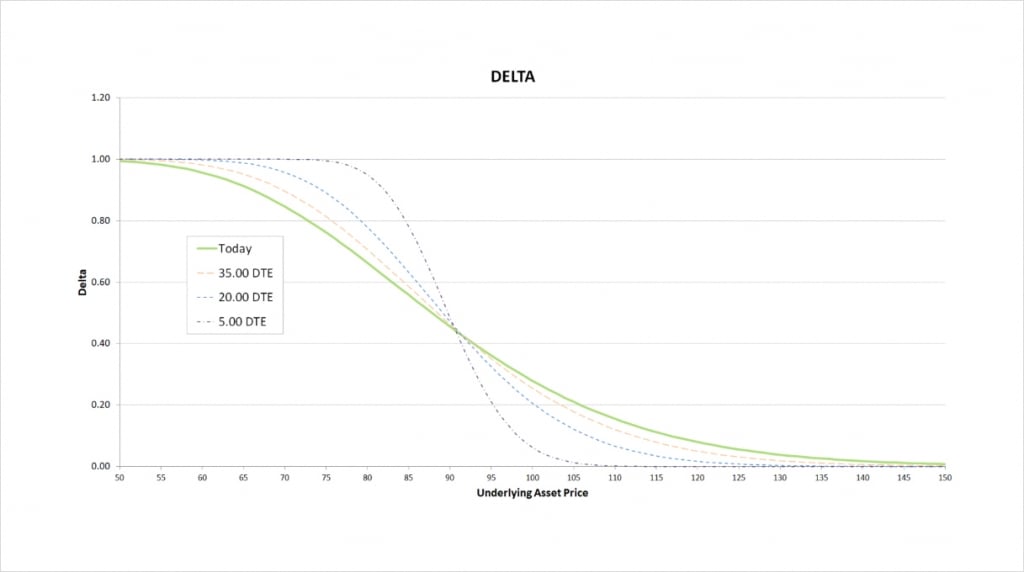
This has the same shape and extreme values of 0 and 1, as the covered call did in the previous lecture.
When the put is deep ITM, it has a larger negative delta. As we are short this gives us a large positive delta. When the put is far OTM, it has a small negative delta, which gives us a small positive delta.
As time passes, if the put is ITM, the delta tends towards -1, so our delta tends towards 1. If the put is OTM though, the delta approaches 0 as time passes instead. It’s when the put is close to the money that we see that delta can change quickly between the two.
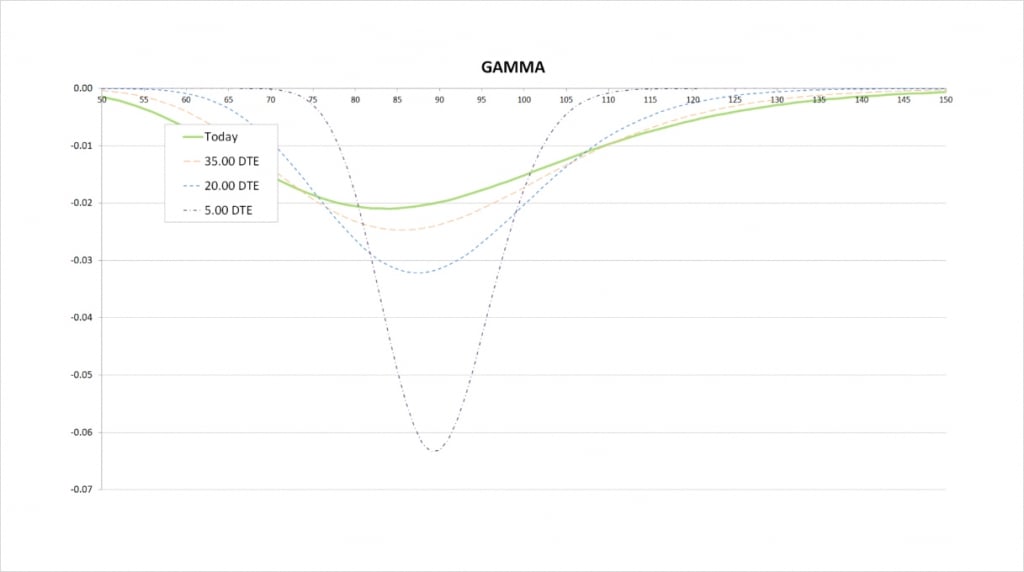
Gamma
As we just saw, the delta for the cash secured put is always decreasing, therefore the gamma is always negative. And due to the characteristics of our delta that we just described, our gamma has the greatest magnitude when the put is close to the money.
Vega
Changes in implied volatility also have no impact on the value of the cash position, therefore when we look at the vega for the cash secured put, we are in fact just looking at the vega of being short the put option.
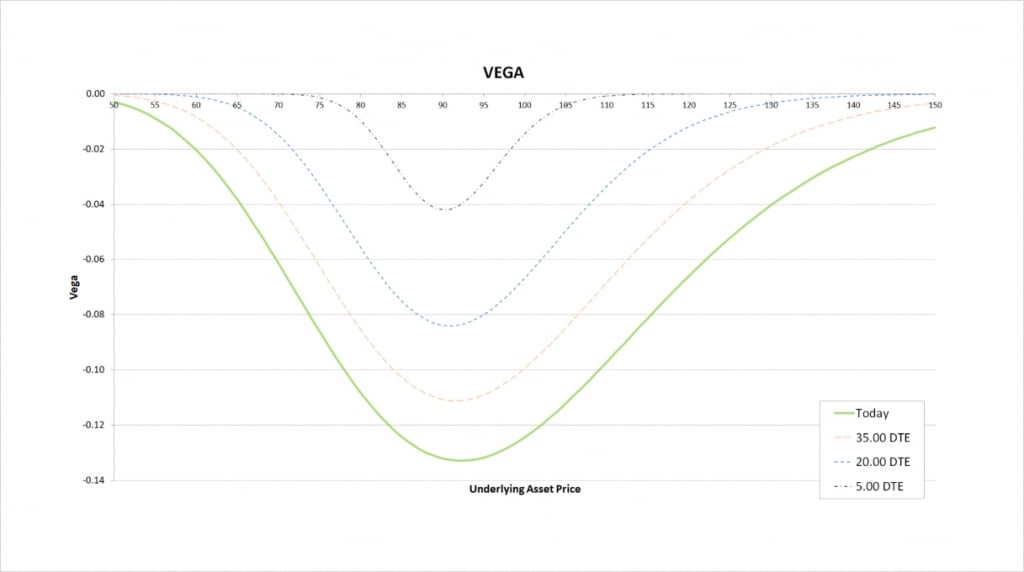
As the seller of a put option, we have negative vega. The magnitude of this vega is greatest when the option is close to the money, and as time passes, the magnitude decreases no matter where the underlying price is in relation to the strike price.
Theta
The put option loses value as time passes, but as the seller of the put here, the loss in value of the put represents a gain for us, hence the positive theta.
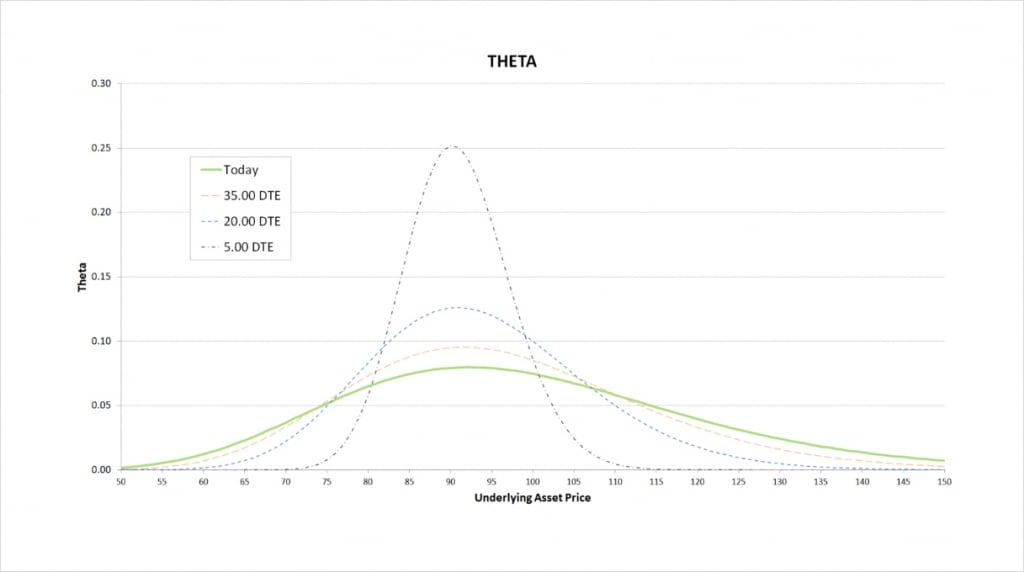
Theta is greatest when the put is close to the money. This is where the put will have the most extrinsic value, and therefore the most value to lose to time decay.
What happens to the theta as time passes depends on where the underlying price is relative to the strike price of $90. When the underlying price is close to the strike price, theta increases as time passes. That is, the put loses value at an ever accelerating rate as time passes. When the put is either deep ITM or deep OTM, the theta decreases as time passes. That is, the put loses its value more slowly as time passes.
Inverse option contracts
As we mentioned at the beginning, some traders mistakenly believe that it’s not possible to execute a cash secured put using the inverse contracts on Deribit, so it’s important to emphasise that this is incorrect, and also to show exactly how this strategy can be executed.
If we look at the payoff chart of a naked short put using inverse contracts, we can see that if we sell a naked put without an adjustment, the account has significant risk to the downside in bitcoin terms.
This chart shows the profit/loss at expiry of shorting a bitcoin put option with a strike price of $40,000, and collecting a premium of 0.04 BTC.
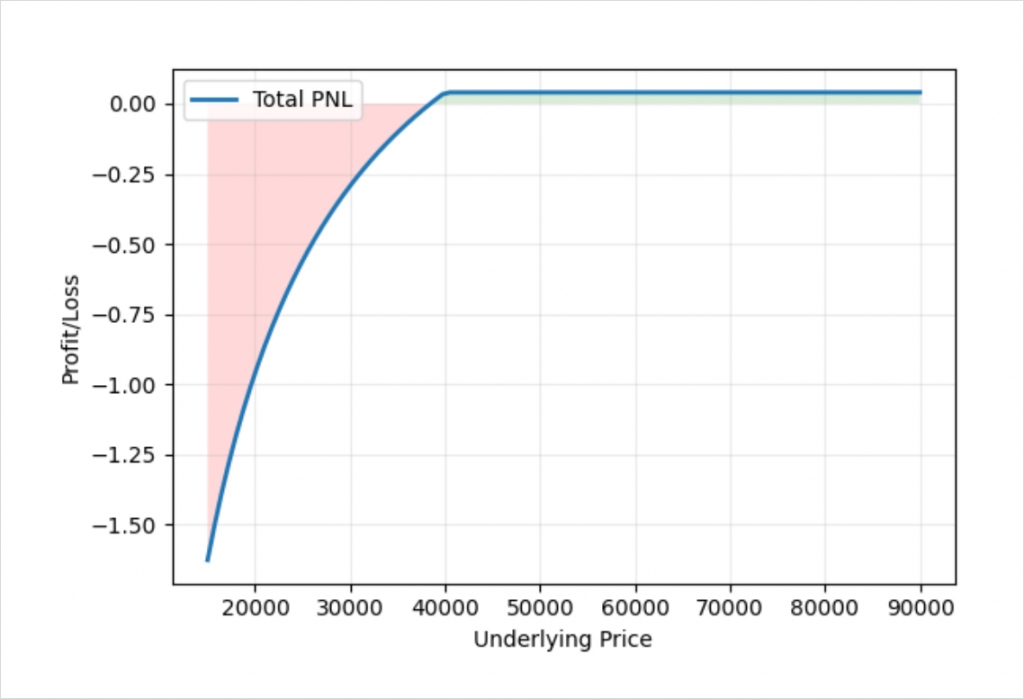
As we covered back in lecture 6.4, when selling a bitcoin put option on Deribit, the maximum loss measured in bitcoin is unlimited. While we do want the risk to be to the downside for a cash secured put, we want it to be linear risk in dollar terms, not unlimited, ever accelerating risk in bitcoin terms.
A cash secured put consists of a short put, and a cash position. The same is true when using the inverse option contracts on Deribit. However, the difference arises when we realise that our account balance on Deribit for trading the inverse contracts is not stored in cash (or dollars), but is instead stored in the underlying asset (such as bitcoin, ethereum or solana). What we need to do then is first enter a position that makes our account behave like cash. In other words a position that (by itself) causes our account to maintain a stable dollar value, rather than a stable amount of the underlying.
Thankfully in practice this is easier than it sounds, and involves a single short future position. We have an entire lecture on just that subject on the Deribit blog here.
If at this point you need a more detailed explanation of hedging the dollar value of an account then feel free to pause here and finish reading/watching that lecture first.
Let’s assume that when we enter this trade the underlying price is $50,000. We want to execute a cash secured put with the $40,000 put and the equivalent of $40,000 in cash. To do this we place $40,000 worth of bitcoin into the account (currently 0.8 BTC), then we short bitcoin with a position size of 0.8 BTC. We can use either the perpetuals or the dated futures. Let’s say we use the perpetual contract this time, which is also trading at $50,000, therefore we short the bitcoin perpetual contract with a position size of $40,000.
By shorting the same value as our account balance, with no additional positions, our account value will now remain stable in dollar terms. This means whether the underlying price of bitcoin increases or decreases, our account will be worth about $40,000. This is perfect as it is similar to the cash position we need to execute a cash secured put.
When we set our account into this synthetic cash state, and then short the put option, it leads to a bitcoin profit/loss chart like this.
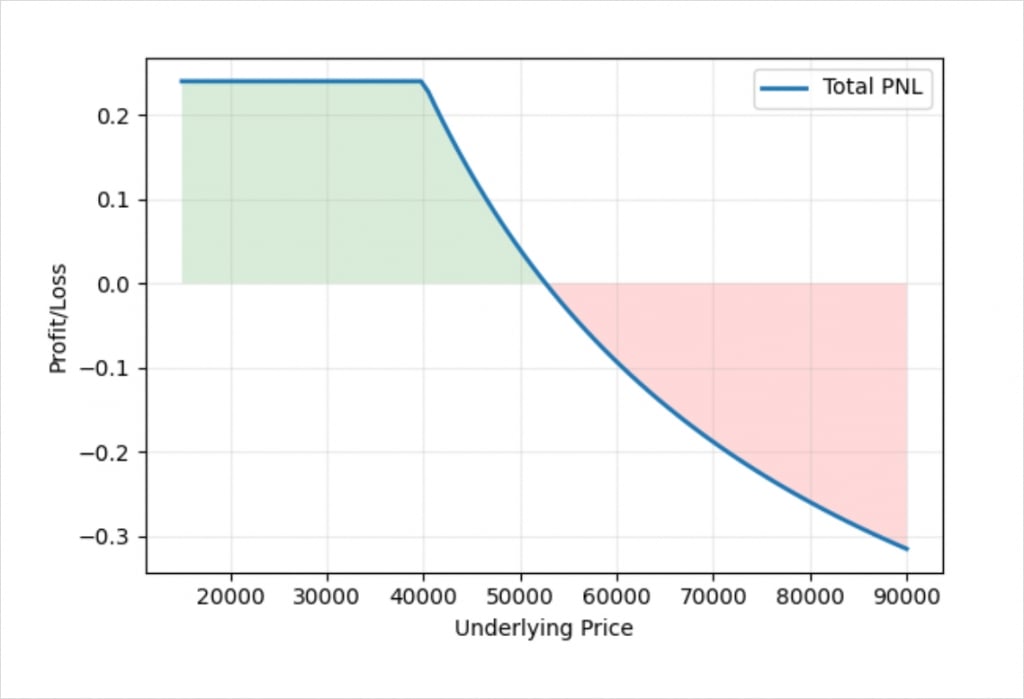
As you can see, we have removed the unlimited risk to the downside. Remember this is the profit/loss in bitcoin terms not dollar terms.
If you remember in the last lecture we introduced the idea of synthetic positions. A synthetic position behaves like one instrument, but is actually constructed using different instruments. This bitcoin profit/loss chart for a short futures and short $40,000 put is equivalent to just shorting the $40,000 call option instead.
So we have eliminated that accelerating bitcoin risk to the downside, and this is the resulting profit/loss in dollar terms.
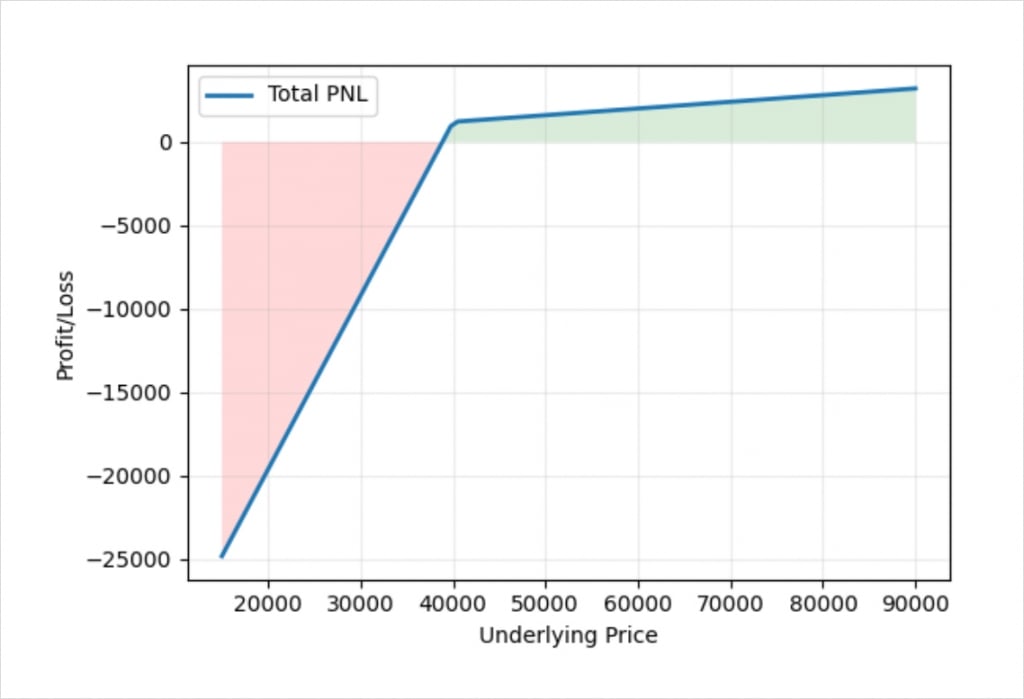
This looks much closer to the usual payoff of a cash secured put that we are looking for. The reason it’s not quite the same yet, and most noticeably why the profit line is not completely flat when the price is above the strike price at expiry, is that we received the credit for selling the put in bitcoin. We have not hedged this extra amount in the futures, so we are effectively still long the 0.04 BTC premium that we collected. This is very easy to hedge as well though if desired, as we can just add an extra 0.04 BTC to our futures short position size. If we do this when we initially execute the trade, we get this profit/loss chart.
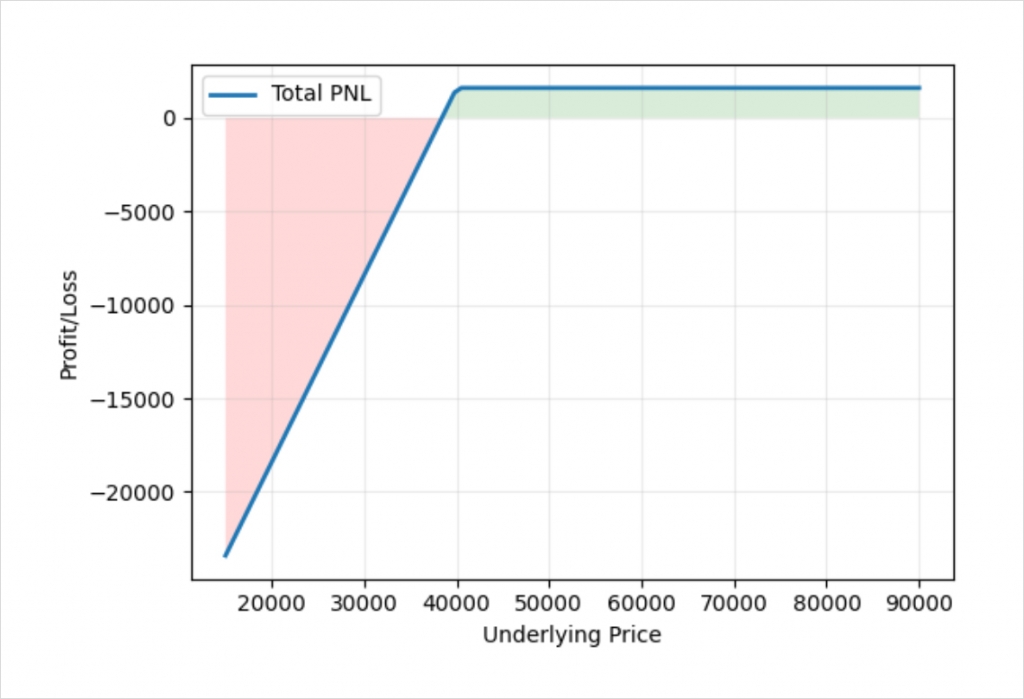
And now we have achieved exactly the same profit/loss that a cash secured put in a more traditional account with linear products would have.
Portfolio margin
As with most portfolios that contain options that at least partially hedge another leg, a cash secured put on Deribit will likely benefit from the portfolio margin system. The portfolio margin system looks at how the entire portfolio of positions in the account would perform with changing market conditions. If the positions hedge each other, as they do with a cash secured put for example, this will be taken into account.
Cash secured puts as a way to purchase the underlying
While the delta of a cash secured put is always positive no matter where the underlying price is, many traders are actually hoping the price does move down at some point in order for them to be able to purchase the underlying cheaper. Some traders like to execute cash secured puts when they are intending to purchase the underlying at the strike price anyway and so are happy to commit to doing so while collecting some premium in the meantime. The logic would be that if they are already committed to purchasing the underlying at that price, they may as well sell a put option and get paid for that commitment in the meantime.
By selling the put option they are giving themselves the obligation to buy the underlying from the put buyer at the strike price, but a credit is received which can be kept no matter what happens. If the put expires worthless, the trader can then sell another put to collect yet more premium while they wait for the price to drop to their desired purchase price. Of course, there is no guarantee that the underlying price will ever fall down to the strike price, or that if it does, that it will subsequently increase.

