In this lecture we will work through some examples of how to calculate the profit or loss of a call option position in dollars. For simplicity, for all of these examples, we will ignore any trading fees. Of course in practice to complete the calculation you would subtract whatever fees you have paid as well.
Profit/loss when closing a call option trade early
When an option position is not held to expiry, but closed early, the profit and loss calculation is very simple. Every trade involves a buy order and a sell order, so you simply subtract what you bought the option for, from what you sold it for.
This is true for both American and European options because we’re talking here about closing a position by selling it to someone else, not about exercising the option.
It is a common misconception that because European options cannot be exercised early, that European option traders are forced to hold their positions until expiry. However, this is not correct.
For example, on Deribit all of the options are European, and therefore cannot be exercised early, but you are still free to close an option position at any time by reducing your position to zero.
If you are long an option, closing the position would be done by selling the option back to another trader, reducing your net position to zero.
If you are short an option, closing the position would be done by buying back the option from another trader, reducing your net position to zero.
Example 1:
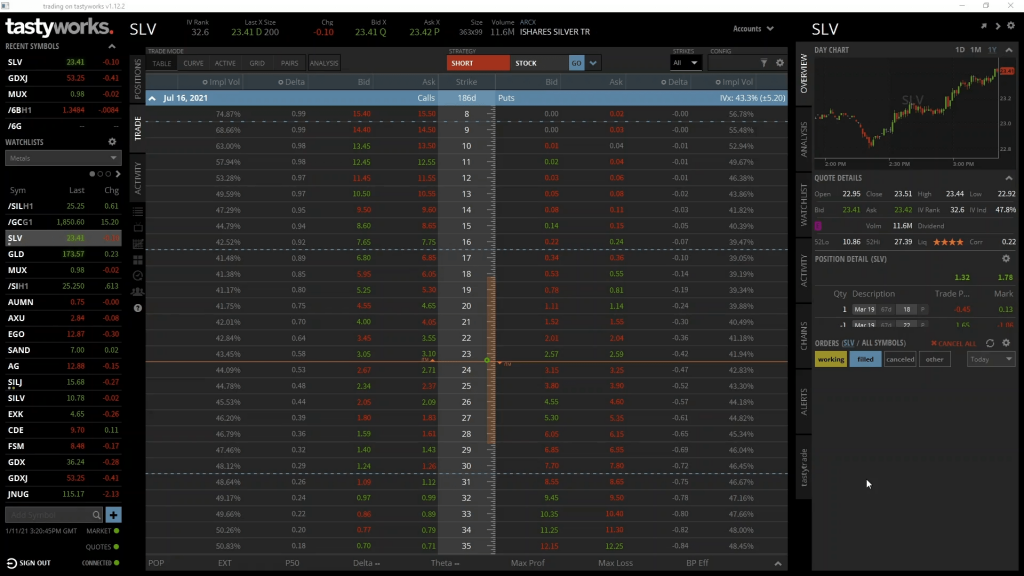
Let’s use a live price on Tastyworks for the example so we start getting used to using the option chain. Here we have the option chain for SLV, which is a silver ETF (exchange traded fund). The precise instrument we’re looking at here doesn’t matter too much for our profit/loss example, except to say that the contract multiplier for SLV is 100. That is, every 1 option contract represents 100 shares of SLV.
One other quick thing to note. We are going to ignore any assignment process for physically settled options in these first few sections. And we will simply calculate the profit or loss in dollars.
As you may remember from the option chains walkthrough lecture, we have strike prices down the centre column, with calls on the left, and puts on the right. We’re only interested in calls for today so we’ll only be looking at the left side of the option chain. Let’s use the call option with a strike price of $30. The ask price, which is the price we can currently buy it for, is $1.26.
So, let’s assume we buy this call option for $1.26 today. How much profit will we make if the price of SLV moves up in the next few days, and the price of this call option moves up to say $5?
It’s worth mentioning that we are not going to go into the specifics of option pricing today and why this option might be worth $5. That will be covered in detail in sections 7 and 8 later in the course.
We’ve purchased this SLV $30 call option for $1.26, and a few days later it has increased in value to $5. We then decide to close the position before expiration by selling it for $5.
The total profit would then be:
$5 – $1.26 = $3.74
Remember though that the contract multiplier for SLV is 100. This calculation of $3.74 profit is per share. As the contract multiplier is 100, the total then is:
$3.74 * 100 = $374.
When we say we bought the call for $1.26, that is per share. For 1 option contract, which represents 100 shares, that brings the total purchase price to $126. Similarly when we sell the contract for a price of $5, that is $5 per share. For 100 shares that is $500.
It’s relatively simple to see that if we bought something for $126, and then sold it for $500, we made a profit of $374. Which is calculated as $500 minus $126.
As we’ve closed the position early, all that matters is the price of our opening and closing orders. The price of SLV at expiry is no longer important to us as our position is now closed.
This is true for all option positions that you completely close early. Your profit is calculated as the price you sold the option for minus the price you bought the option for.
Options held to expiry
At expiration, all of the extrinsic value of an option resulting from volatility and time is gone. To calculate the value of an option when held to expiry we just need to know the strike price and the delivery price at expiration. This gives us the value of the option at expiration, then we simply adjust for the premium paid.
Let’s use the same $30 call option on SLV from example 1, but now we will assume we hold it until it expires.
When a call option has some value at expiration, i.e. when the underlying price at expiration is greater than the strike price, we can calculate the profit/loss of the option position at expiration using this formula:
(Price At Expiration – Strike Price – Premium Paid) * Contract Multiplier * Number Of Contracts
We can plot this formula for different values of ‘Price At Expiration’, which gives us this profit/loss payoff chart.
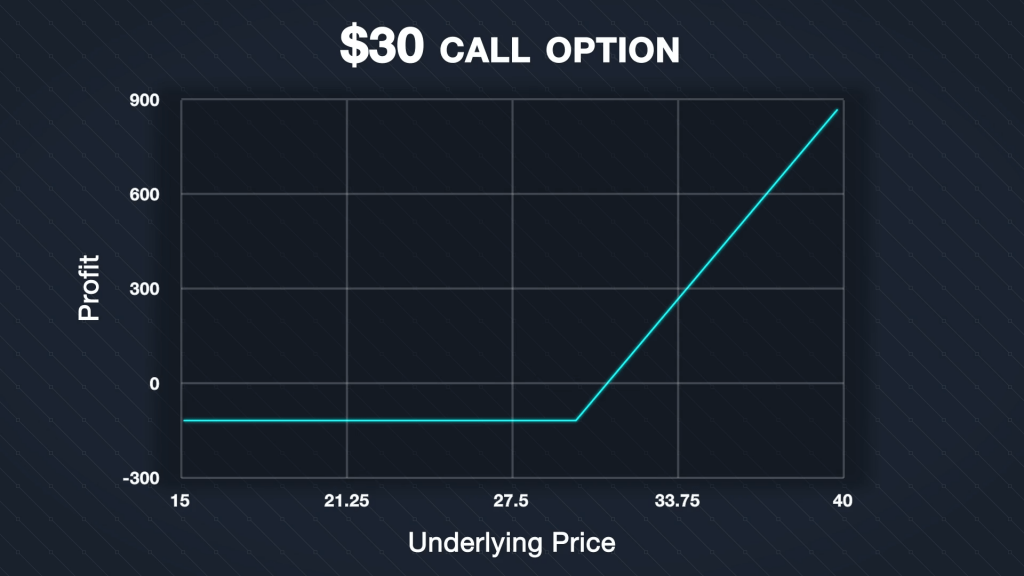
We will be using these types of PNL charts a lot throughout the course. They are a great way to visualise any option position, including multiple options together. They make it very simple to see exactly where your risk and profit potential is.
As you can see, for this call option at expiration, the risk is fixed to $1.26 if the price of SLV is anywhere under $30. The profit then increases continuously for any SLV price above $30. Let’s look at some specific examples.
Example 2:
So, this time we’ve purchased the $30 SLV call option for $1.26. Let’s assume that the price of SLV at expiration is $38.
This means we have:
- A price at expiration of $38
- A strike price of $30
- A premium paid of $1.26
- A contract multiplier of 100, and
- A number of contracts of 1
Substituting all these values into the formula, we get:
(38 – 30 – 1.26) * 100 * 1
=6.74 * 100 = $674
That’s $6.74 per share, multiplied by 100 shares.
This long call option position has therefore made a profit of $674.
Example 3:
Using the same option again, what if instead, the price at expiration was $31.
We would then have:
- A price at expiration of $31
- A strike price of $30
- A premium paid of $1.26
- A contract multiplier of 100, and
- A number of contracts of 1
Substituting all these values into the formula, we get:
(31 – 30 – 1.26) * 100 * 1
=-0.26 * 100 = -$26
That’s negative $0.26 per share, meaning this long call option position has instead made a $26 loss.
Notice here how the price at expiration of $31 was above our strike price of $30. This means the call option did have some value at expiration, $1 per share to be precise. However, because we paid $1.26 per share for the option, the value at expiration was not enough to make up for the premium paid, leading to a small loss.
Example 4:
Sticking with this same call option, let’s finally see what happens if the price goes in completely the wrong direction, and assume the price at expiration is $20.
We would then have:
- A price at expiration of $20
- A strike price of $30
- A premium paid of $1.26
- A contract multiplier of 100, and
- A number of contracts of 1
This time though, we don’t need to use the formula because the call option has no value. This is because the price at expiration is below the strike price.
The loss is simply what was paid for the option, which is:
Premium Paid * Contract Multiplier * Number Of Contracts
1.26 * 100 * 1 = $126
Even though the price of SLV dropped way below the strike price of $30, the loss of the long call option position is limited to the price paid for the option. Even if the price of SLV had dropped to zero, the loss would still only have been $126. This fixed risk is one of the most attractive features of buying options.
In summary
Buying a call option has a fixed risk. The maximum loss is limited to the premium paid for the call option. This maximum loss will occur when the option is held to expiration, and the underlying price fails to rise above the strike price by this time.
When closed early, the profit/loss of a long call option is equal to the price it was sold for minus the price paid for the option.
When the call option is held to expiry, and the underlying price is greater than the strike price, we can use this formula to calculate the profit/loss precisely:
(Price At Expiration – Strike Price – Premium Paid) * Contract Multiplier * Number Of Contracts
The further above the strike price the underlying price has moved, the more profit a long call option will make.

