Deribit Position Builder – Primer on basic option strategies

By now as a Deribit trading participant you are familiar with call and put options – sell an option and collect the premium in return for giving up PnL on an adverse price movement, or buy an option to profit if you are right on the size of a price movement. As a refresher, here is our Education article on this.

For the purposes of this article we will focus on call option strategies in general, please keep in mind that everything discussed here for call option strategies applies to put option strategies except the payoff direction is reversed.

Naked options

Here we will introduce the payoff diagram at option expiration in more detail, using the Position Builder tool on Deribit. You can play around yourself with it here.

For the purposes of this article we will look at PnL in USD terms (you can set this on the chart by clicking on the 3 dots and toggling “PNL in USD”). We will also look only at the payoff diagram at option expiration by dragging the time to expiry bar all the way to “Expiry” as shown in the call diagram below:

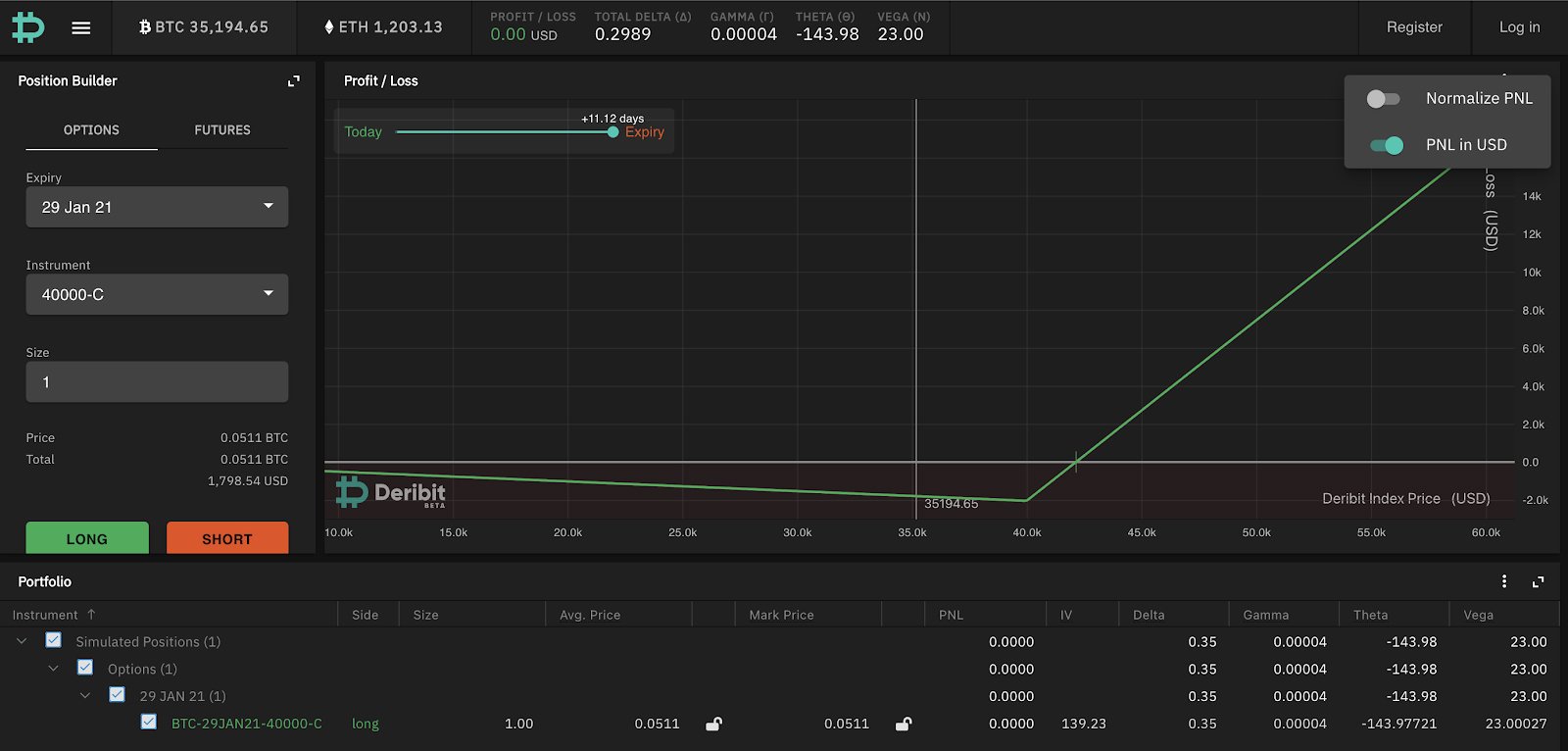
A couple of notes about the payoff diagram above (for buying a Jan 40k call with BTC spot at 35194.65) :

• If BTC rises over the 40k strike the payout in USD is linear (the payout will be settled in BTC on Deribit at the expiry BTCUSD price).
• If BTC remains below the 40k strike you can see that the USD loss on the position decreases as BTC falls. This is because the premium you paid for the call is paid in BTC and it is converting this BTC premium into USD to calculate the overall PnL. Of course, at the time of entering this trade you have paid BTC equivalent to a USD value at the current price (sold BTCUSD through the premium paid). You can hedge this exposure on entering the trade by buying back the amount of BTCUSD, so in reality you can consider your USD PnL loss as unchanging up to expiry (so the slope of the curve can also be considered to be flat rather than negative).

Synthetic futures

You can create an synthetic long future (a “synthetic”) by buying a call and selling a put on the same strike, as follows:

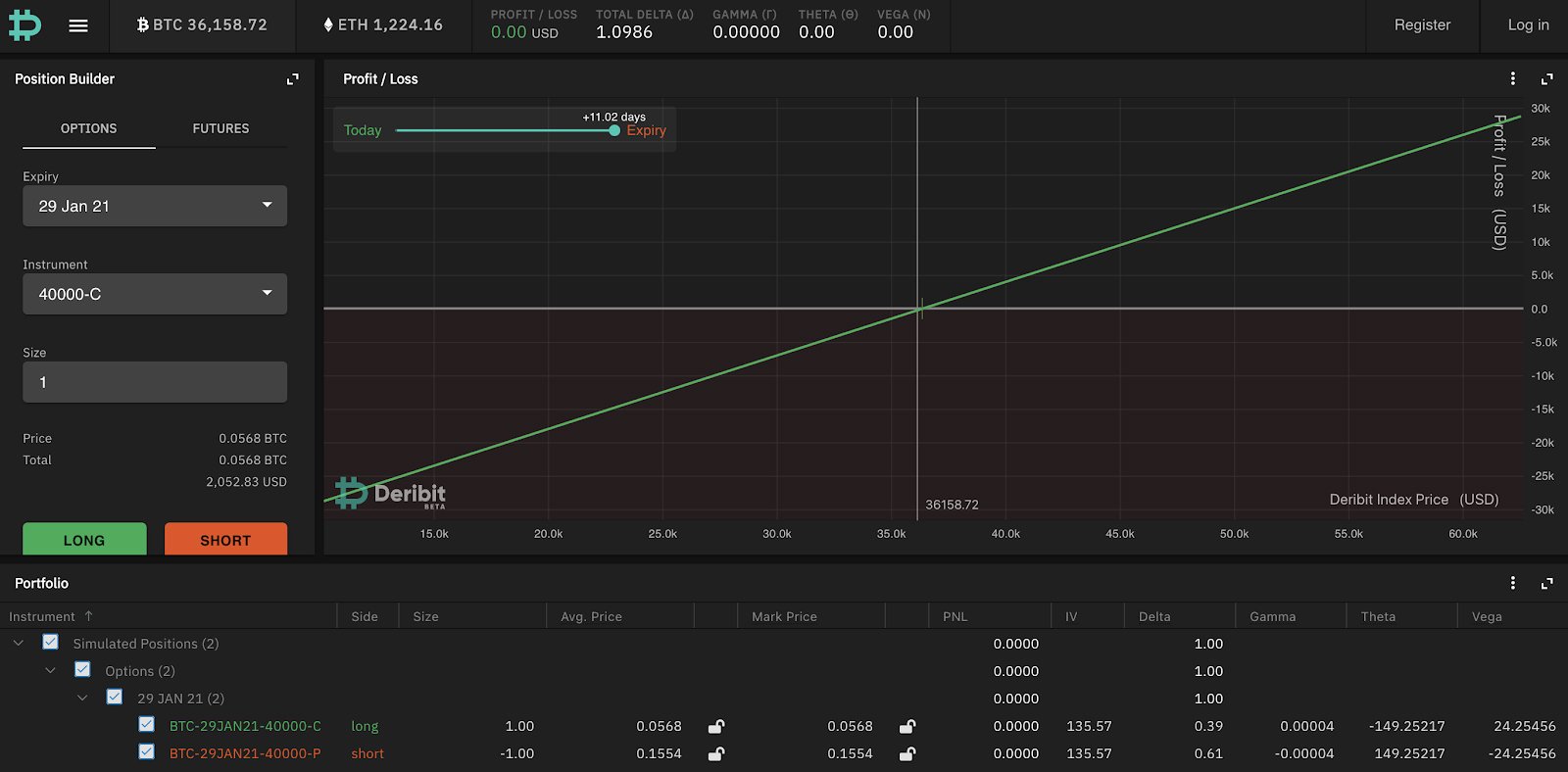
Note that because you have bought an option and sold an option on the same strike and same expiry the payoff diagram is completely linear and has no convexity, so you have no volatility exposure.

One reason that you may want to do this is if you want to neutralise your volatility exposure on a prior option trade. For example, if you bought a Jan 30k call a while ago and BTC moved up to 35k, the Jan 30k call is now in the money and very illiquid. If you want to sell the volatility exposure you don’t need to sell the Jan 30k call – what you can do is sell the same amount of Jan 30k puts instead which brings your payout profile to a linear one as above and simply decide to hedge as much of the combined delta as you want using perpetual swap or futures.

Put-call parity

In payoff exposure terms, a synthetic future (C – P) is equivalent to long spot or long futures aside from the premium you paid to create the position. What this means from a practical viewpoint is you can convert a call into a synthetic put and vice versa simply by delta hedging 1:1.

For example:

Long 1 call + short 1 synthetic future = +C – (C – P) = P
Since a synthetic future is equivalent in payoff to an actual future or spot, this also means that Long 1 call – 1 BTC = P

There are some nuances to this that are too technical for this discussion but assuming all positions have the same expiration date and all option premia are hedged this is accurate – try to recreate these positions on the Position Builder and see for yourself!

Spread

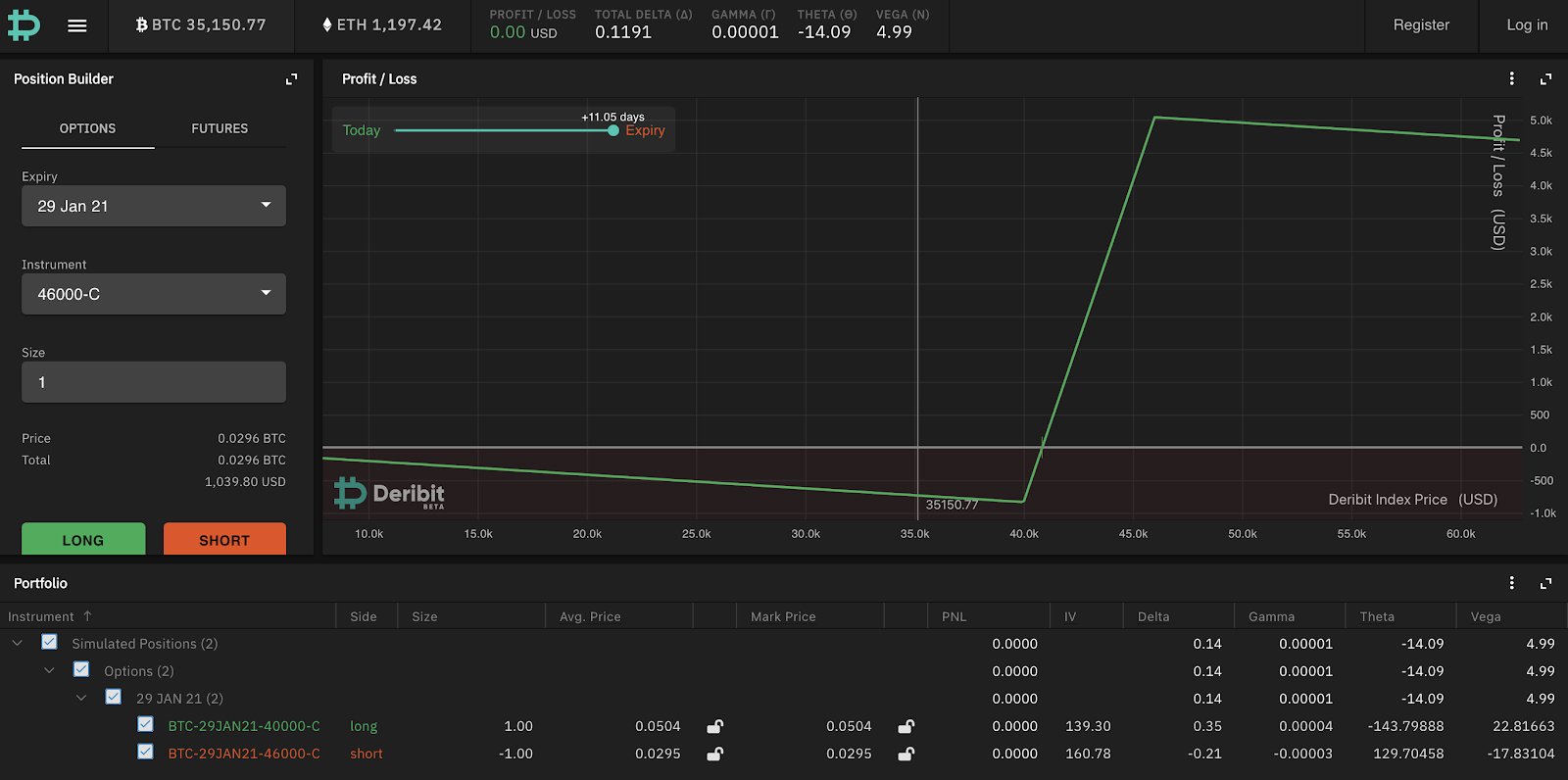
A long call spread is where you buy a call option on a lower strike and sell an option on a higher strike. The PnL chart of the 40k-46k call spread is shown here (again, ignore the gradient of the chart for expiry price < 40k and > 46k which is due to the value of the premium paid).

By buying a lower strike call and selling a higher strike call you make money if BTC rises above the lower strike on expiration but cap your gains to the higher strike. The main motivations for buying this are that you are bullish but only to a certain extent – since this is buying an option while selling another one this reduces the premium paid if you are wrong on the trade.

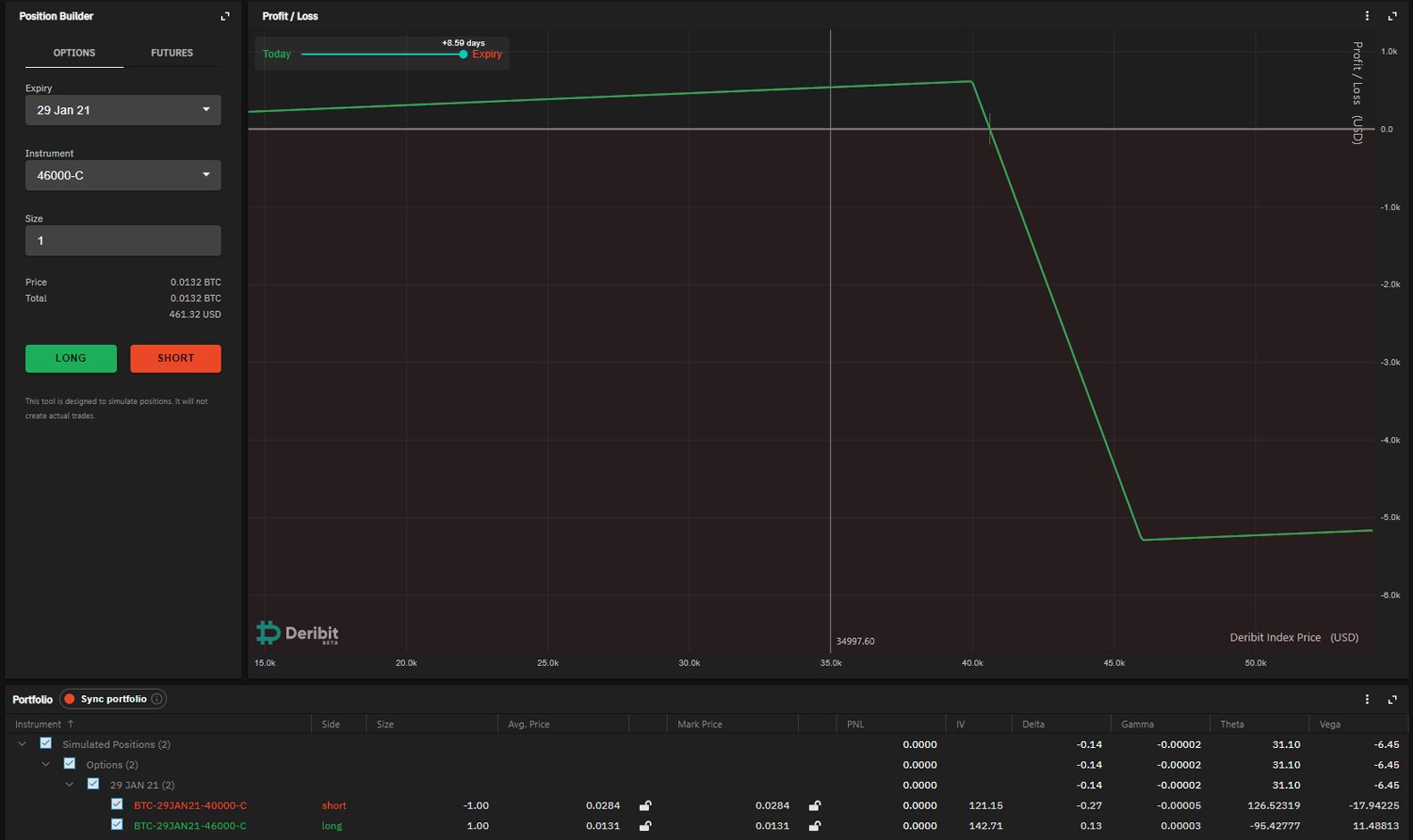
Similarly, this is the payoff diagram for selling the same call spread – you collect a smaller premium for selling this but your losses are capped to the upside if you are wrong.

Due to put-call parity, a long call spread payoff is identical to a short put spread payoff with options on the same strikes and vice versa, as shown below:

Long 40k/46k call spread:
40k C +1
46k C -1

Sell 40k synthetic and buy 46k synthetic (so delta neutral):
40k C -1, 40k P +1
46k C +1, 46k P -1

Sum of these positions = short 46k/40k put spread:
40k C 0, 40k P +1
46k C 0, 46k P -1

Straddle

A straddle is where you buy a call and a put on the same strike. The payoff diagram is as follows:

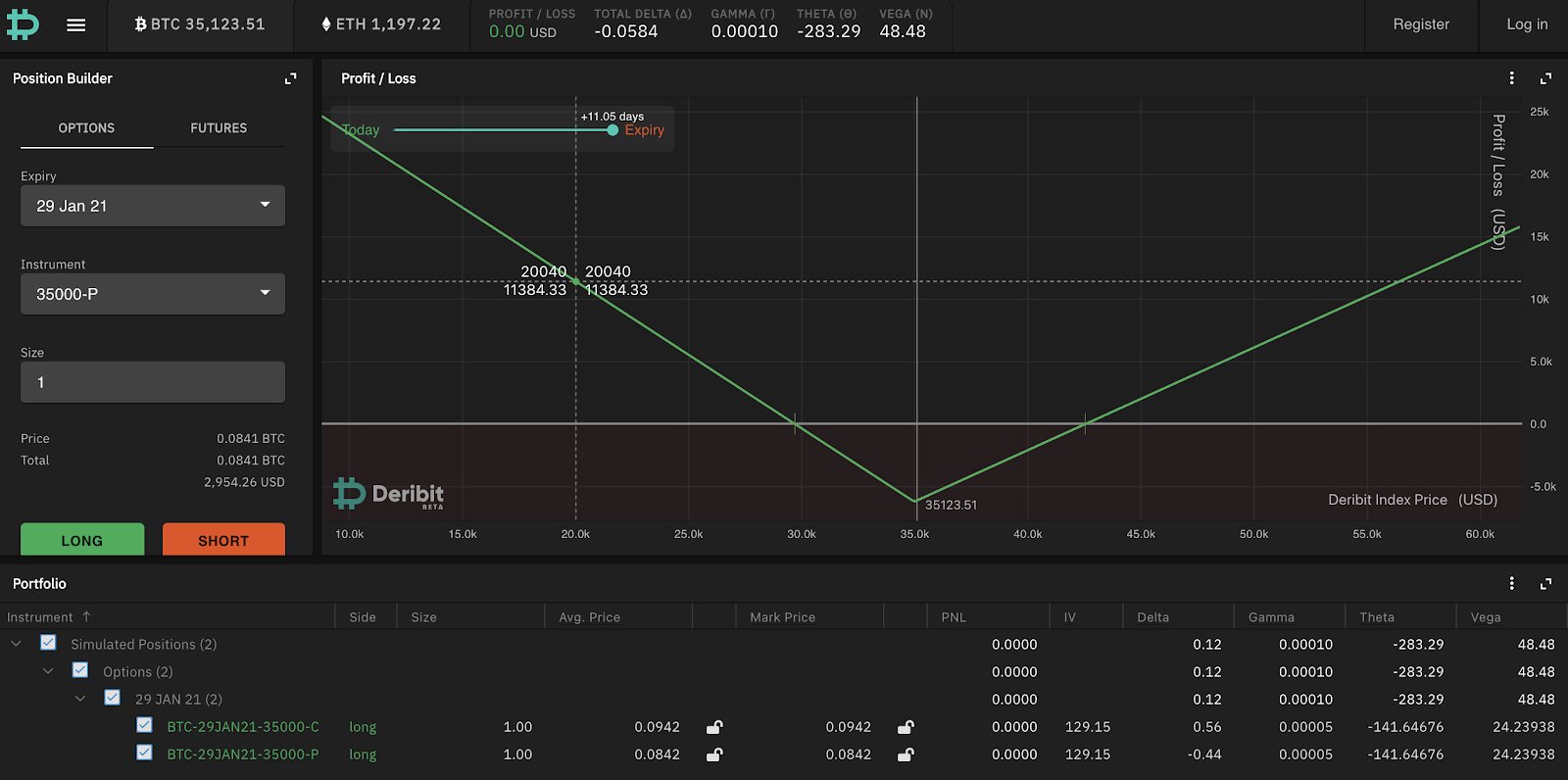
By buying this strategy, your bet is that BTC will move further away from the strike on expiration than you paid in option premium (i.e. you are long volatility).

Conversely, if you are short a straddle:

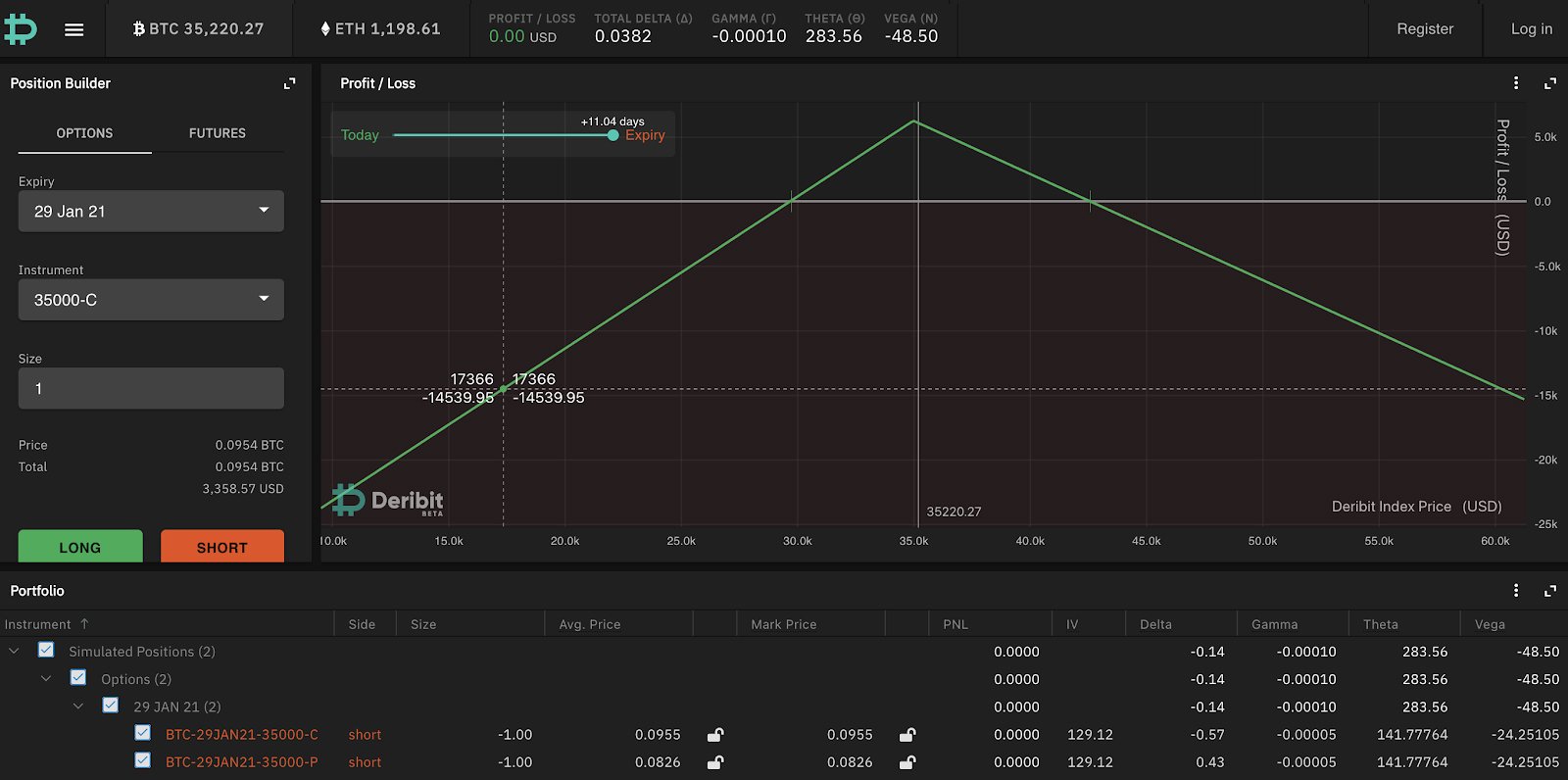
You can see here that your maximum payoff is at the strike where both options in the straddle expire worthless and you collect the entire premium that you sold the straddle for. The further BTC moves away from the strike the more you lose.

Strangle

A strangle is similar to a straddle in that you buy a call and a put, but the options are on different strikes (put strike < call strike). As you can see from the payoff diagram, by buying a strangle you are also betting that BTC will move far away, however you don’t make any profit until it goes through either strike. This is offset by the fact that the strangle options are further away from ATM so you are paying less in option premium for the strangle than the straddle.

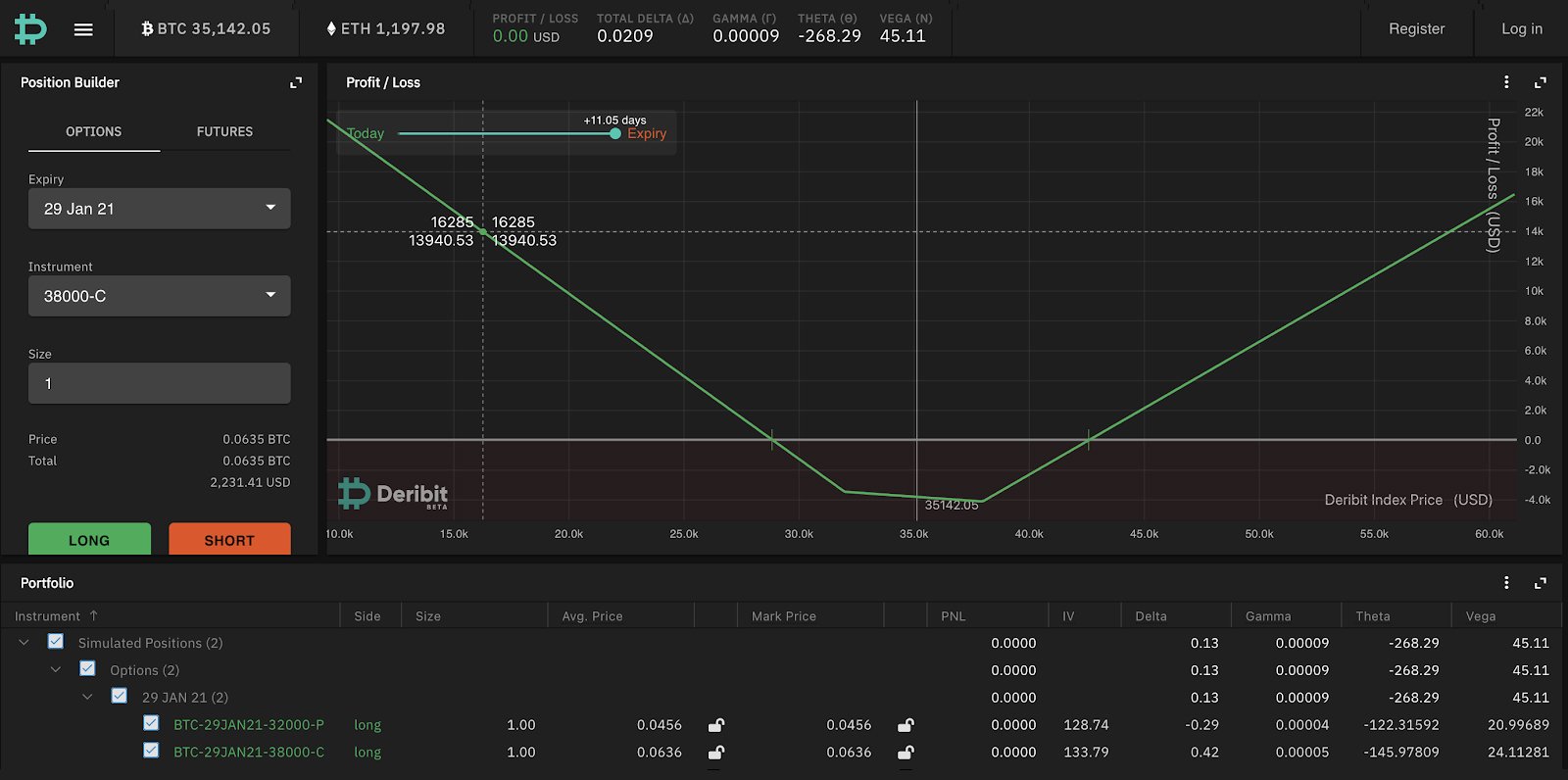
Shorting the strangle has the same considerations – you collect less in premium but you don’t start losing money until BTC moves further away:

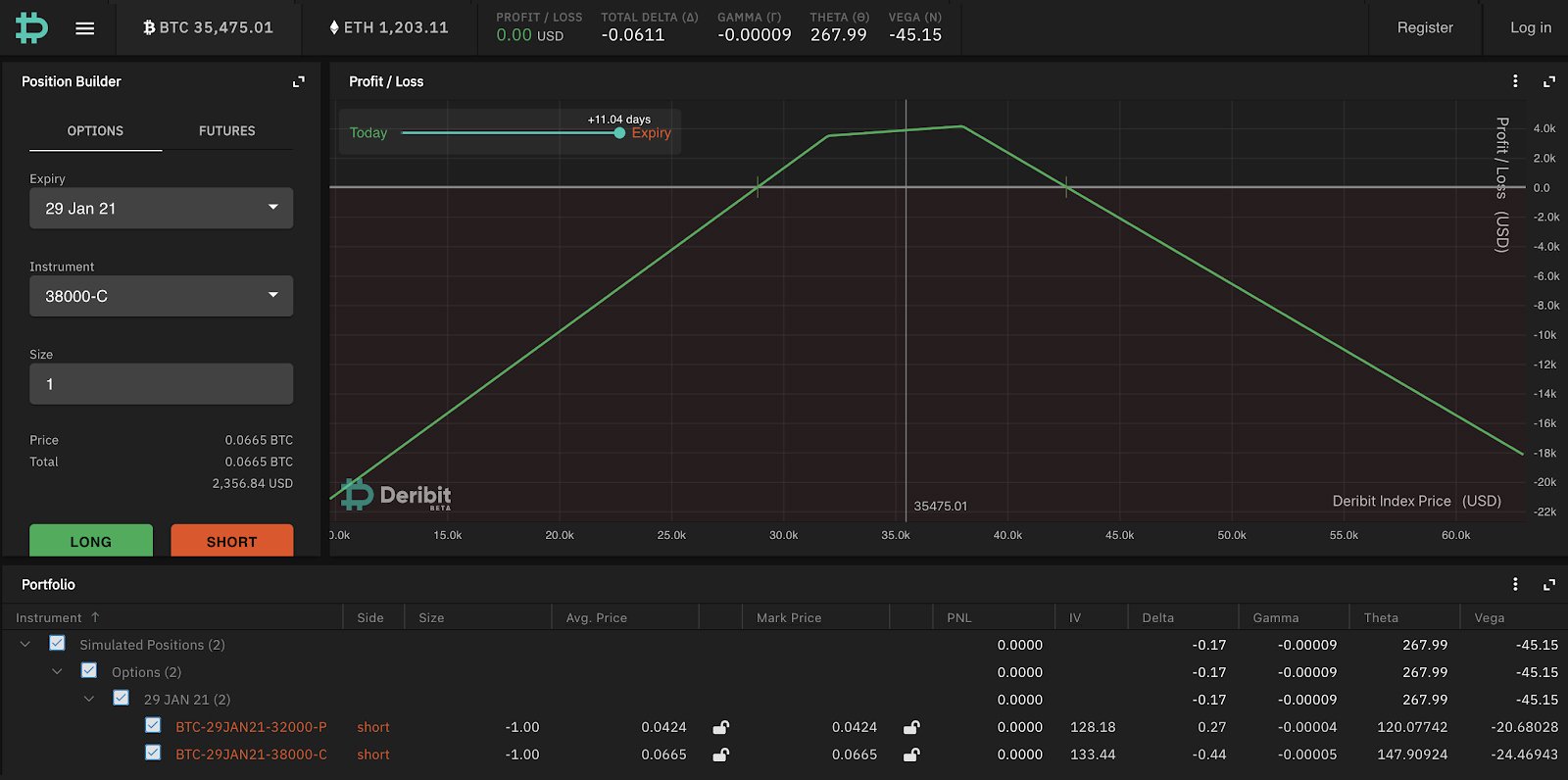
Butterfly

The butterfly (colloquially known as a ‘fly’) is a strategy that allows you to bet on a relatively specific outcome on expiration. The payoff diagram for the 40k/46k/52k butterfly is as follows:

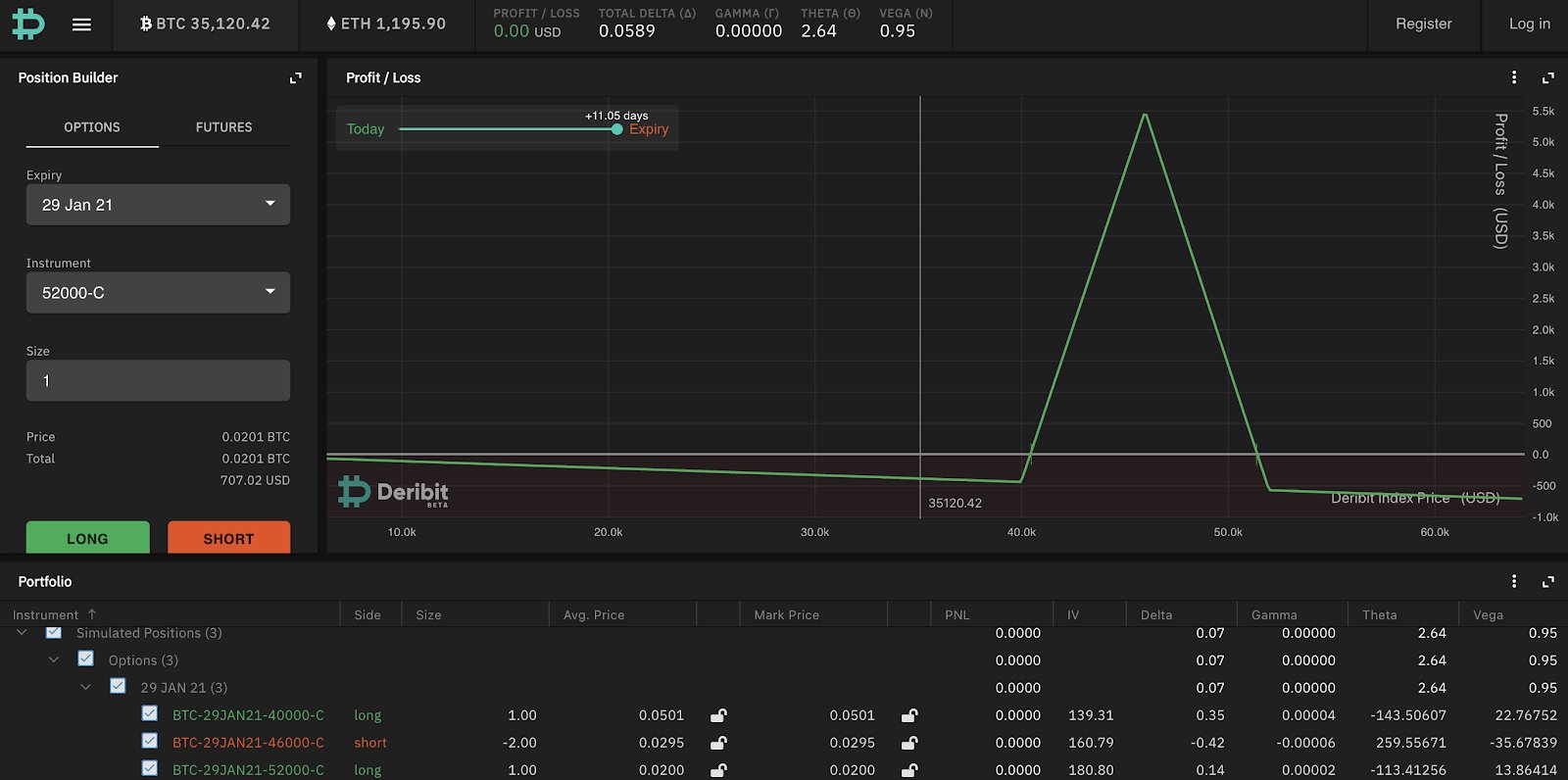
You can see in the diagram that by holding this position your most profitable outcome (ignoring the premium paid) is if BTC expires close to the middle options strike (max payoff = the gap between the strikes) and your least profitable outcome is if BTC is outside the wide strikes where your payoff is 0. Because of this, a butterfly should always be worth >= 0 since you can only profit from holding one and never lose aside from the premium paid.

Taking a look at the actual options position in this structure you can see this is formed by:
40k C +1
46k C -2
52k C +1

Where the gap between the strikes is symmetrical.

You can break this down into combinations of other strategies mentioned earlier:

With spreads:
Long 40k/46k call spread =
40k C +1
46k C -1

Short 46k/52k call spread =
46k C -1
52k C +1

So the butterfly = buying a lower call spread and selling a higher call spread where the middle strike is shared and the strike gaps are the same.

The same payoff diagram can be achieved using straddle and strangle:

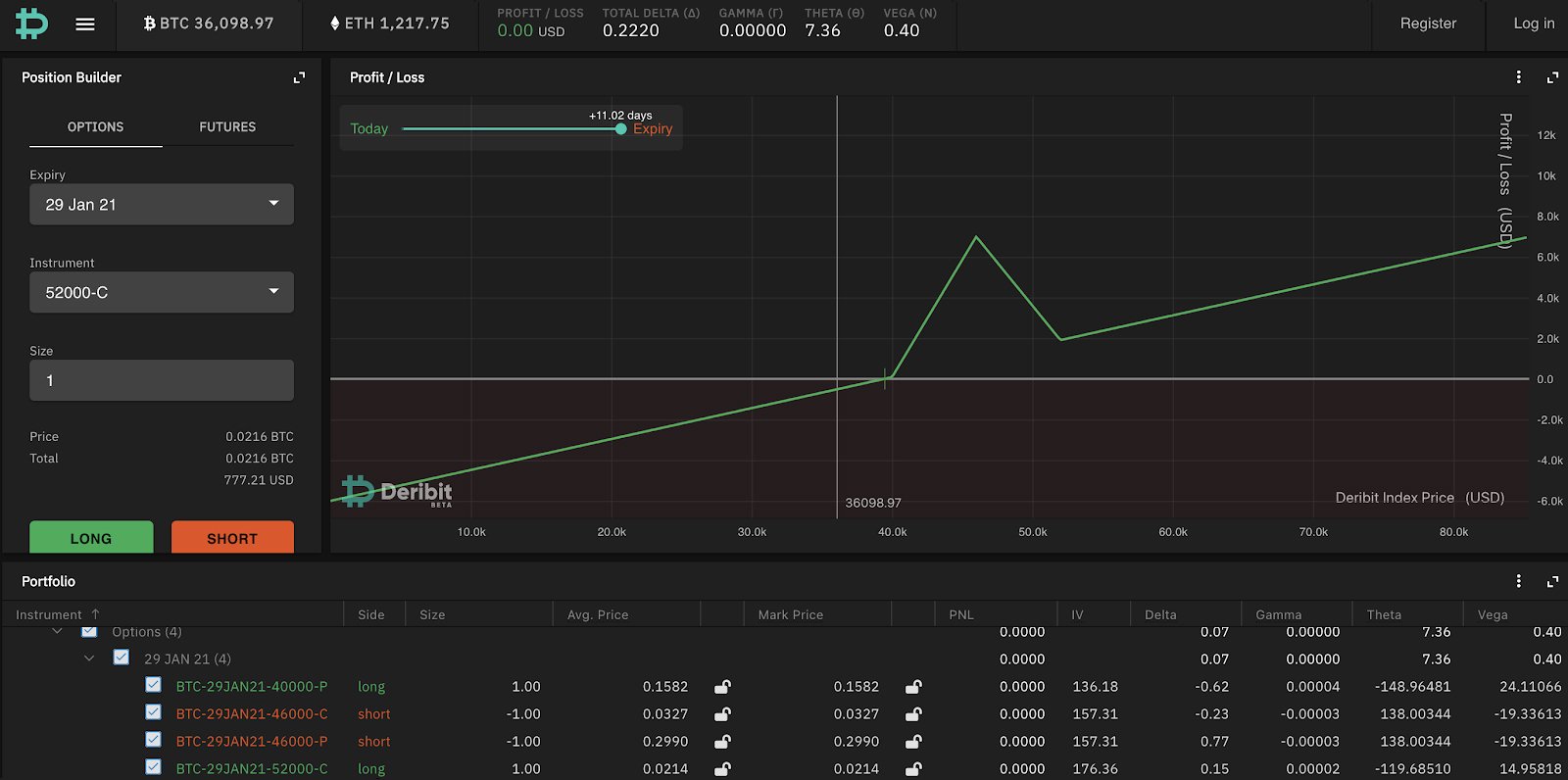
Long 40k/52k strangle =
40k P +1
52k C +1

Short 46k straddle =
46k C -1
46k P -1

The difference in the slope of this graph vs the slope of the call butterfly graph is only due to the difference in option premium paid (shown as unhedged) because we are using puts rather than calls so the option prices are different.

Note that this combination can also be conceptualised as selling a put spread + selling a call spread with the same middle strike:
Short 46k/52k call spread =
46k C -1
52k C +1

Short 46k/40k put spread =
46k P -1
40k P +1

As discussed above, a long call spread is equivalent to a short put spread on the same strikes through put-call parity, so the payoff is equivalent to a butterfly.

Conclusion

This has been a brief introduction to basic option strategies and using the Deribit Position Builder tool to visualise payoffs. If you choose to adopt any of these strategies you will be able to use combinations of options to profit from more specific outcomes than just trading naked options and manage risk more tightly.