Option Model Delta and Its Considerations

The definition of delta is the sensitivity of the option price to a move in the underlying (= change in the price of the option/change in the price of the underlying asset). It can be viewed as the probability that the option will be in the money by expiration. Since most of the options’ pricing is based on the Black-Scholes model or some variation of it, this discussion will revolve around the practical effects of this model.

One important thing to note is that because the Black-Scholes options pricing model is simply a mathematical model, the accuracy or ‘correctness’ of its output is determined by:

• how well the chosen model fits the market that it is applied to
• the correctness of the inputs

It is useful to keep this in mind, as the model is simply a tool for analysing option prices and not a source of truth.

Impact of Forward Price

With respect to the calculated delta of an option, the Black-Scholes model calculates the theoretical forward price of the underlying asset as the current spot price discounted by the risk-free interest rate until the option expiry. In practice, in traditional markets, large institutional players arbitrage significant pricing deviances of futures from their theoretical forward prices. Cost of funding tends to be similar for large market participants, therefore futures contracts tend to trade close to their theoretical value unless there are structural impediments in the market.

In crypto, however, futures pricing can deviate significantly from the trader’s theoretical forward price for a variety of reasons (e.g. prevailing bullish/bearish sentiment, lack of liquidity, cost of funding can differ significantly between market participants).

As a result, for options pricing, a trader can choose to use a forward price as the underlying input that reflects current futures prices as opposed to their theoretical spot vs interest forward price. If the futures price used is higher than the theoretical spot forward price, then a call option delta based on the futures price would be higher than the one based on spot, and put delta would be lower (less negative).

Different traders can see the same option price and calculate a different delta on their position as a consequence of using a different forward price (or equivalently, a different interest rate).

Impact of Volatility Smile

The Black-Scholes model is based on the assumption that the returns of the underlying asset follow a lognormal probability distribution (illustrated below):

Note that the shape of this distribution has the following conveniences in terms of reflecting market price moves:

• At the end of the period the underlying price cannot go below zero
• The ‘fatness’ of the distribution on the downside reflects a higher likelihood of big crashes compared to big rallies
• The underlying price is more likely to remain at the current level than to move a lot.

Of course, this is simply an assumption based model to simplify the calculation, but this is the shape of the probability distribution if you calculate every single strike option using the same implied volatility input.

However, reality doesn’t necessarily conform to this probability distribution (reality, in this case, is the market perception of the true probability distribution of the underlying price). The true market perception is demonstrated by supply and demand, so how do options traders incorporate it in the model (which represent the market belief of how the probability distribution differs from lognormal)? By changing the price of the option! It is easier to use the same model to calculate every option price rather than changing the model itself. Especially, as every input into the model for different strike options is the same, aside from the implied volatility. Therefore, the only way to incorporate this into the option pricing for each strike is to have each strike be priced with different implied volatility. Hence what is known as the volatility smile:

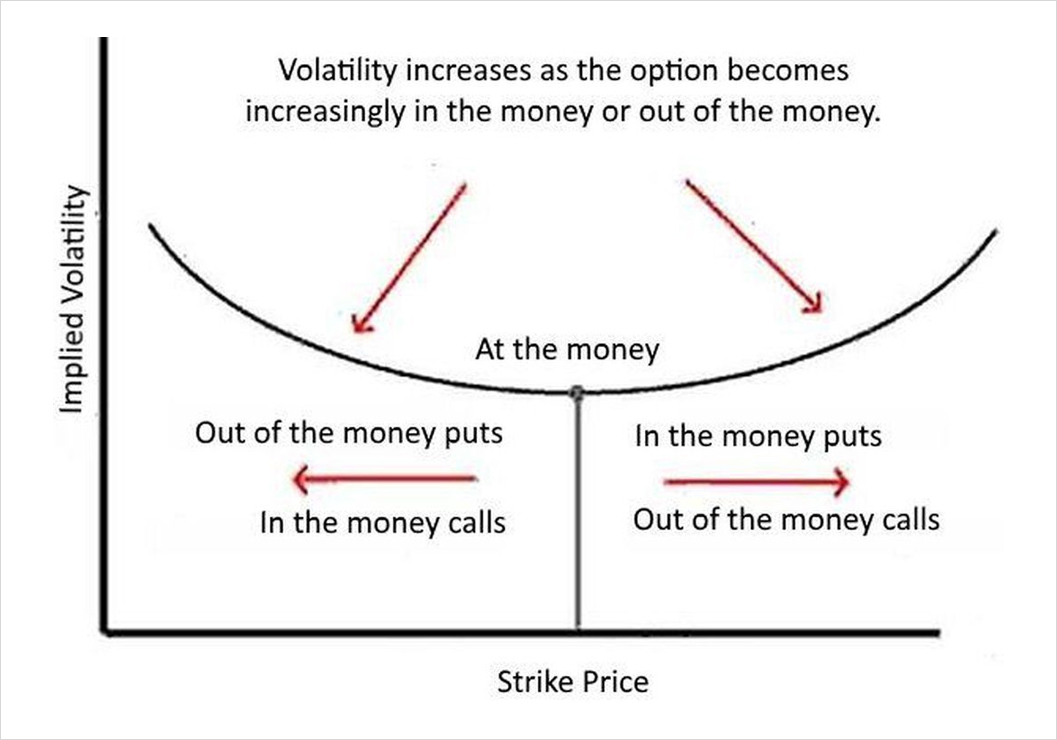
You can see this in the IV columns for calls and puts in the following Deribit BTC options screen:

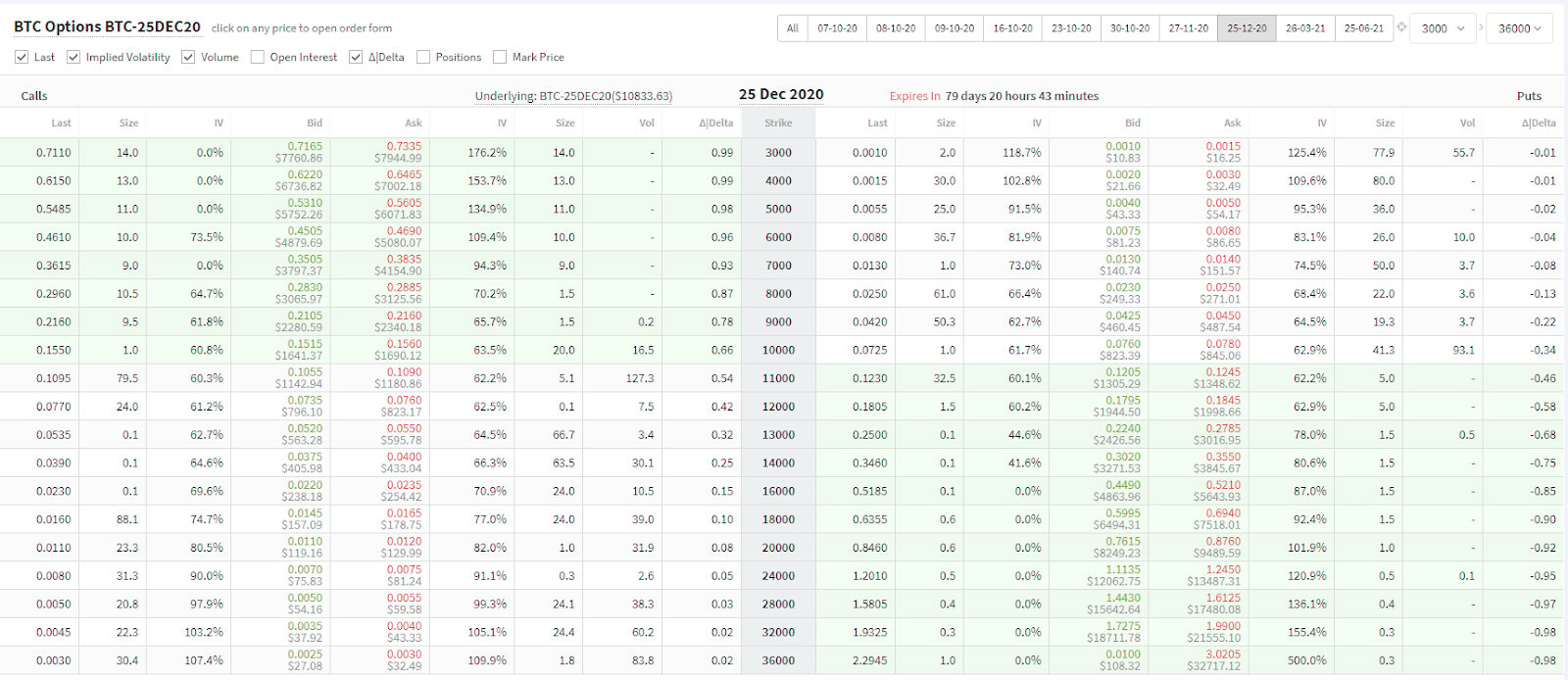
So how do we interpret this? This reflects that the market is willing to pay for a higher probability of a big move compared to the default lognormal distribution (i.e. that the market distribution has fatter tails):

Another way that the options pricing can reflect the market expected distribution compared to the lognormal distribution is with skew – which is a difference of implied vol for upside strike vs downside strikes. If upside options are more expensive (have higher implied volatility) than downside options this is known as positive skew (so the market thinks the price is more likely to go up), and vice versa.

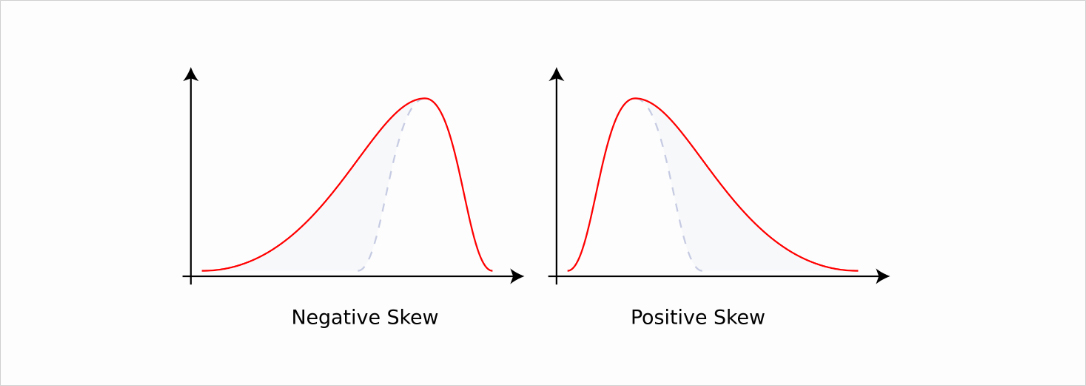
So how does this impact the delta of options? If the implied volatility of out of the money options goes up, this means that the market is pricing a higher probability that it will be in the money by expiration, and therefore the delta of the option will go up (in an absolute sense). Conversely, for an in the money option if the implied volatility goes up the delta will go down (since it’s already in the money, it becomes more likely to go out of the money by expiration). Note that this means the delta of an option changes constantly based on supply and demand of the option, which is reflected in the pricing.

In conclusion, two ways in which calculated option delta can change or observed differently by different traders are the use of a different forward price and the use of a different implied volatility input for that option.