So far in this section, we have only discussed the vega of individual options, but most option traders are likely to have positions/portfolios consisting of more than one option contract at a time, and they will want to know the vega of their entire portfolio. They will also want to know how their total vega will evolve as time passes, or as other parameters change, such as the underlying price. All of this information will help them gauge how their options will be affected by changes in implied volatility.
As with the other Greeks we have discussed so far in this course, it is possible to sum the vega of each individual option in the portfolio to get the total vega.
Multi leg example – bull call spread
Let’s look at a simple multi leg option position, a bull call spread. This position consists of purchasing one call option, then selling another call option with a higher strike price, but both with the same expiration date.
This chart shows the vega of a $100/$110 bull call spread (in green), and of the two individual options that combine to create this spread. The $100 call option (in blue) is purchased, and therefore gives us positive vega, meaning it will gain value if IV increases. However, the $110 call option (in red) is sold, and therefore gives us negative vega, meaning the increase in value of this option when IV increases, will actually represent a loss for us.
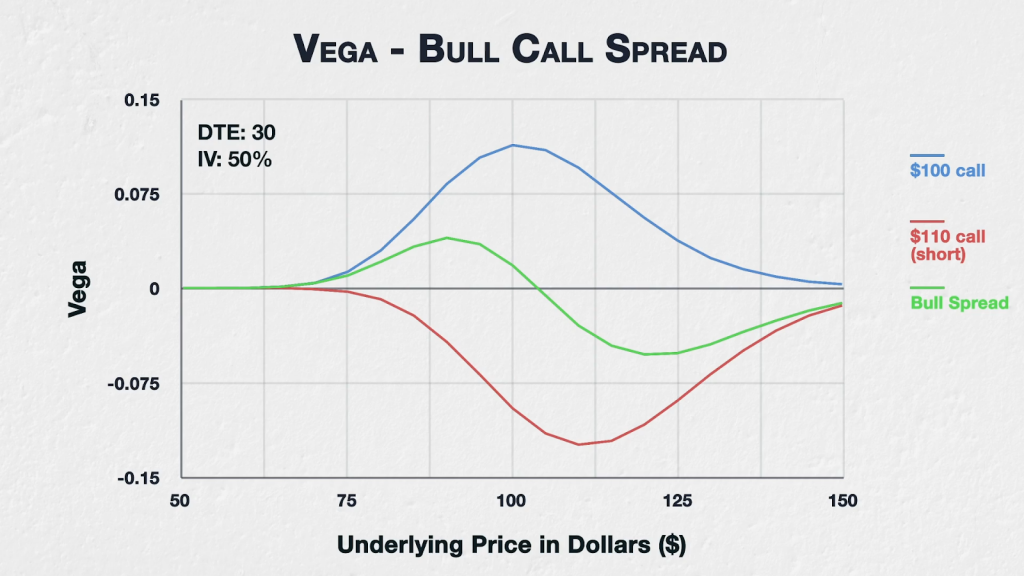
The bull spread line is simply the sum of the vega for the $100 call long and the $110 call short. Whether the vega is positive or negative for the spread, depends on where the underlying price is in relation to the strike prices.
Starting on the far left, with the underlying price down at $50-65, both options are so far OTM that they both have hardly any sensitivity to changes in IV. Vega is therefore very small for both individual options, and also the spread as a whole.
Moving right to the $70-$95 area, both options are still OTM, but are closer to the money and therefore have picked up some vega. The $100 strike is of course quite a bit closer and so picks up more vega sooner. If we take the underlying price of $90 as an example, the long $100 call has a vega of 0.0826, and the short $110 call has a vega of -0.0426, which means the spread has a total vega of 0.04. The vega is positive, meaning if the underlying price is sitting at $90, the spread will currently gain value if IV increases.
Once we get to an underlying price of $100, the $100 call is ATM, while the $110 call is still OTM. The vega of the $100 call peaks here, while the $110 call is still gaining more vega. As we are short the $110 strike, this means although the vega of the spread is still positive, this value is now decreasing.
By the time we get to an underlying price of $110 and beyond, the vega for the spread is negative. This means the spread will now lose value if IV increases. This is because with the underlying price above both strikes, the $110 call will gain more value from an increase in IV than the $100 call will. As we are short the $110 call, this results in the spread losing value.
Then finally to the far right of the chart, both options are now deep ITM and have very little sensitivity to IV changes again. Vega is therefore very small for both individual options, and also the spread as a whole.
We’ve used a vertical spread here, but the same holds true for other spreads, and any other option combination you can think of. Underlying price movement, implied volatility, and time will all still have an effect on the vega of multi leg option strategies, just as they do for individual options. To get the total vega for all the legs combined, we can simply sum the vega for all the individual legs.
Notice also, that even though IV changes still have an effect on the spread, because the vega of each leg partially cancel each other out, the magnitude of the effect of IV is considerably less than for either of the individual options.
Position size and vega
To keep things simple we have so far assumed a position size of one. This will rarely be the case in practice so you will often need to know the vega for positions that vary in size.
To calculate the vega of a position size that does not equal one, we simply multiply by the position size to give the total vega of the position.
The bitcoin options on Deribit have a contract multiplier of one, meaning each option contract represents a notional position of one bitcoin. With this in mind let’s look at a few examples of calculating the total vega, taking into account the position sizes.
For example if you purchase 5 bitcoin call options with a vega of 0.05 each, the total vega of your position is $0.25. This is calculated as:
5 * 0.05 =$0.25
This means you would expect the position to gain $0.25 if IV increased by 1% and all else remains equal.
If you purchase 20 calls with a vega of 0.12, and purchase 20 put options with a vega of 0.09, the total vega of your position is $4.20. This is calculated as:
(20 * 0.12) + (20 * 0.09)
= $2.40 + $1.80
= $4.20
This means you would expect the position to gain $4.20 if IV increased by 1% and all else remains equal.
And finally if you purchase 10 options with a vega of 0.16, and sell 10 options with a vega of 0.22, the total vega of your position is -$0.60. This is calculated as:
(10 * 0.16) + (-10 * 0.22)
= $1.60 – $2.20
= -$0.60
Remember we have sold the second leg here, so the position size is -10, rather than just 10. This gives us negative vega for that leg, and the total position also now has negative vega. This means you would expect to lose $0.60 if IV increases by 1% and all else remains equal.
Summary
The vega of a multi leg option strategy is equal to the sum of each of the vegas for the individual options it contains. Remember to also adjust for the position size by multiplying the vega of the option by the position size.


