In this lecture we will be looking at back spreads and front spreads, this time both with puts. A put back spread is the opposite of a put front spread. For us to execute a back spread position, the trader on the other side of the trade would be by definition executing a front spread, and vice versa (assuming both legs are traded as a single position).
A put back spread is a bearish strategy, and therefore gives us a negative delta. The put back spread is constructed by:
-Selling a put option with strike price B
-Purchasing 2 put options with strike price A, where B > A
The underlying price will typically be at or above B.
The put front spread is just the opposite of this. So we would instead buy a put at strike B, and sell 2 puts at strike A.
In both cases, both of the puts have the same expiry date, and the underlying price is typically somewhere at or above B.
Ideally we would collect a small credit when establishing the position, however this won’t always be the case so we may pay a small debit instead. If we do manage to establish the put back spread for a credit, this gives us a payoff chart that looks like this.
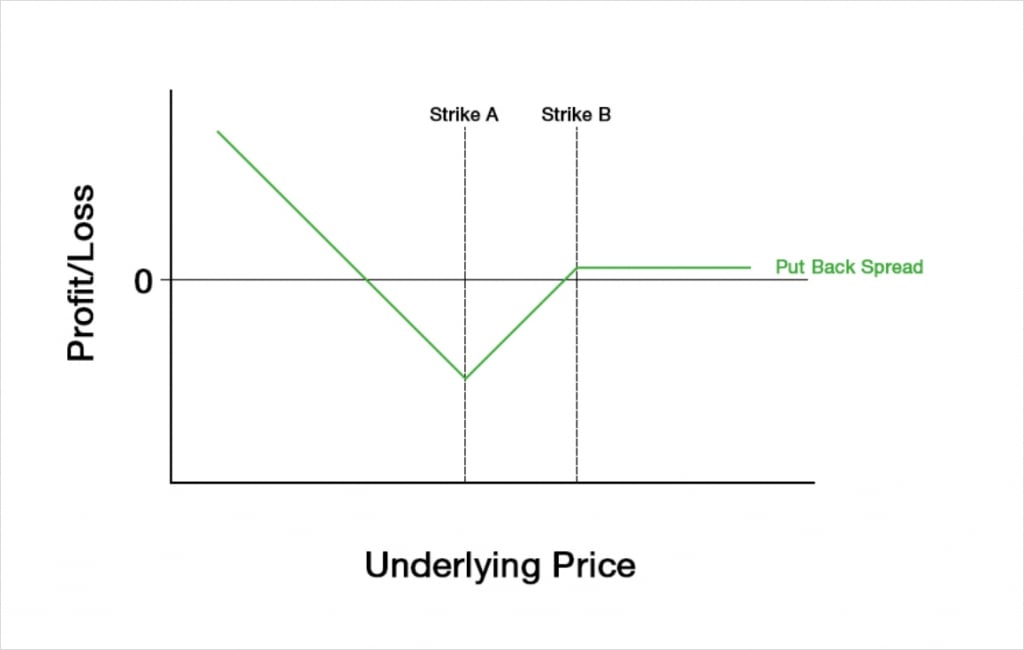
The maximum loss of the put back spread is fixed, but can still be large. The maximum loss is equal to:
Maximum loss = Strike B – Strike A + X
Where X is the net amount we pay to establish the position. If we receive a credit instead then this number (X) will be negative, and will have the effect of decreasing the magnitude of the maximum loss.
The maximum loss occurs when the underlying price is precisely equal to strike A at expiry.
The maximum profit to the downside is only capped by the underlying price reaching zero, but the underlying price needs to decrease significantly for a large profit to be made at expiry. One of the attractive features of a back spread is that if we are completely wrong on the direction, our risk is minimal, and we may even make a small profit if the strategy is established for a net credit. When established for a credit, we also make a small profit if the underlying price is above strike B at expiry.
When established for a net credit we also have two breakeven points. In dollar terms, the breakeven points can be calculated as:
First Breakeven = Strike B – Credit received
Second Breakeven = Strike A – (Strike B – Strike A + X)
Where X is the net amount we pay to establish the position. The Second part of the calculation in brackets here is equal to the maximum loss we mentioned earlier.
If instead of receiving a net credit, we pay a net debit to establish the position, then we only have the second breakeven point. The first breakeven point will no longer exist as the PNL line no longer crosses the x axis into profit to the upside.
These breakeven points are shared by the opposing put front spread, but the profit and loss are of course flipped around the x axis.
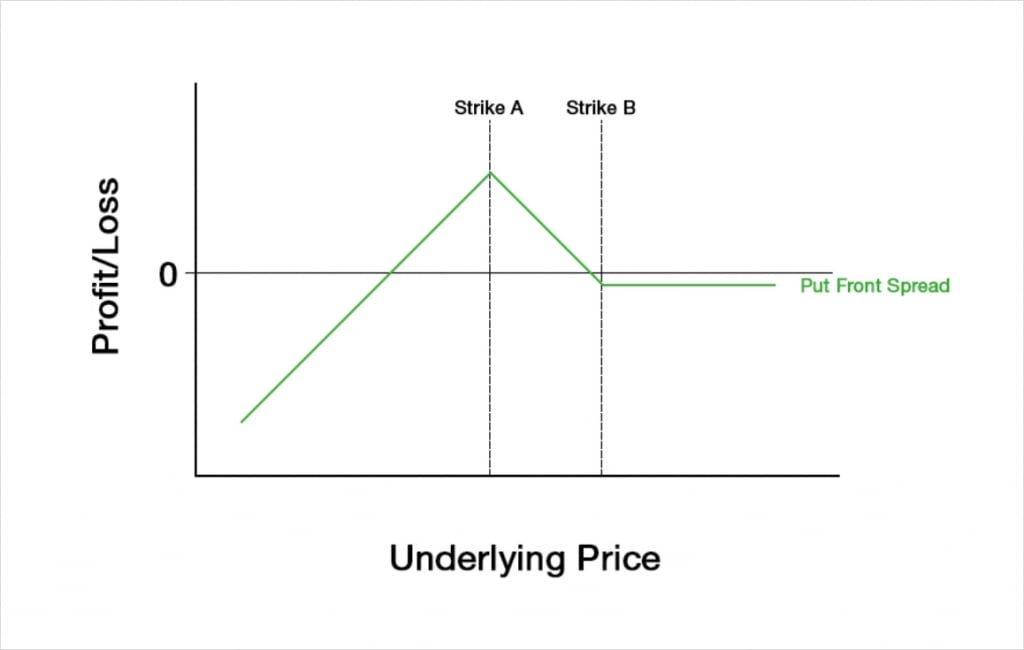
We’ve just flipped our example PNL around the x axis here so the front spread has been established for a net debit, but ideally we would also want to establish a front spread for a net credit if possible. For the front spread, this will be easier when OTM options are being priced higher in implied volatility terms than the ATM options. When this is the case, the 2 options that we are selling that are further OTM will be priced higher in IV terms, so we should collect a larger premium for them than if the volatility smile were flatter.
With a front spread, as we are short 2 options and only long 1, a decrease in implied volatility will be good for us in most situations. Conversely for the back spread, as we are long 2 options and only short 1, an increase in implied volatility will be good for us in most situations.
The Greeks
For the following sections on the PNL and the Greeks, we will focus on the values for the put back spread. To get the values for the put front spread, we just need to multiply by minus one. This just changes the sign of any value, and as always, any gain for the buyer is a loss for the sell, and vice versa.
We can add our Greek values for the put at strike B to the values for the puts at strike A, and this will give us the total Greek values for the put back spread.
To analyse how the Greeks behave we will use the following figures:
Underlying price: $100
Time to expiry: 50 days
Interest rate: 0
Implied volatility: 60%
Strike A: $80
Strike B: $90
Profit and loss
With these parameters the $90/$80 1×2 put back spread will initially give us a credit of about $1.06. The payoff chart looks like this.
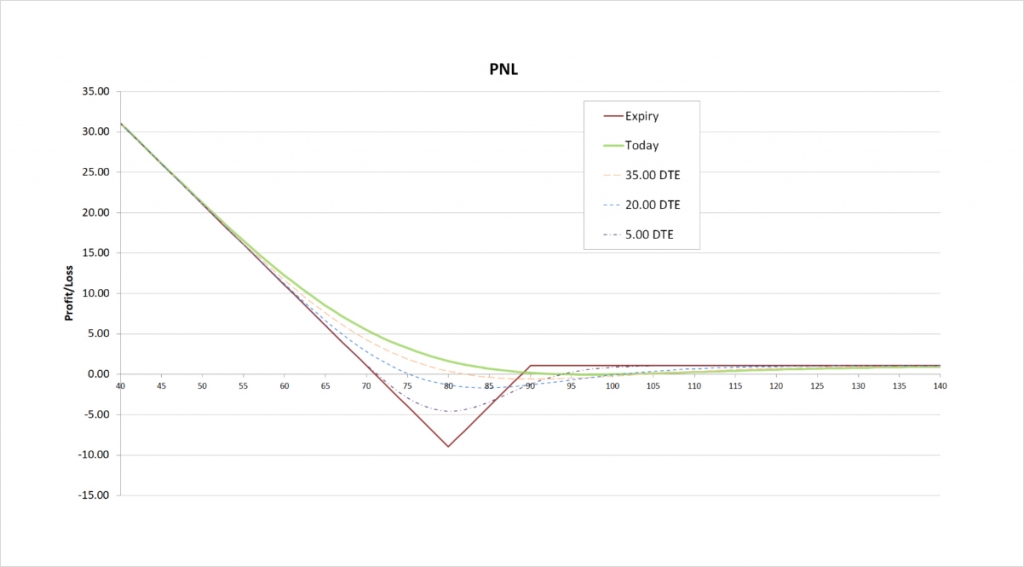
The maximum loss is capped by this formula that we gave earlier. Where X is the net amount we pay to establish the position. We received a credit so X will be negative.
= Strike B – Strike A + X
= 90 – 80 – 1.06
= $8.94
This maximum loss occurs when the underlying price is precisely at strike A ($80) at expiry.
As we collected a net credit for the put back spread, we will make a small profit if the underlying price is above strike B ($90) at expiry. This profit is limited to the credit received of $1.06. The potential profit to the downside is only capped by the underlying price reaching zero.
As we have collected a credit, we have two breakeven points.
First Breakeven:
= Strike B – Credit received
= 90 – 1.06
= $88.94
Second Breakeven:
= Strike A – (Strike B – Strike A + X)
= 80 – (90 – 80 + (-1.06))
= 80 – 8.94
= $71.06
The seller on the other side of the trade, who has the corresponding front spread, has the same breakeven points, but they have a fixed maximum profit and unlimited risk to the downside.
Delta
The put back spread is a bearish strategy, and as such the delta is mostly (but not always) negative.
This chart shows the delta of the put back spread, with the x axis being the underlying price. The extra lines also show how the delta will evolve as time passes.

When both of the puts are far ITM, our delta is very close to -1. The delta then moves closer to zero as the underlying price increases, and is very close to zero when both options are far OTM. When the position is first placed, the delta looks similar to that of a single long put option. This is logical as we are net long one put option.
As time passes though, the delta line rises further into positive values when the underlying price is just below our short strike of $90. By looking at the profit/loss chart we can see why this is the case. As we get closer to expiry, the risk is that the underlying price will end up close to our long strike of $80. As expiry approaches, if the underlying price is sitting close to our short strike of $90, there is not much time left for the price to decrease significantly, so a small decrease in price just makes it more likely we are going to suffer a bigger loss, hence the positive delta in this area.
Gamma
When the position is first opened, as we move from left to right on the delta chart, the delta of the put back spread is (almost) always increasing. This means the gamma is (almost) always positive.
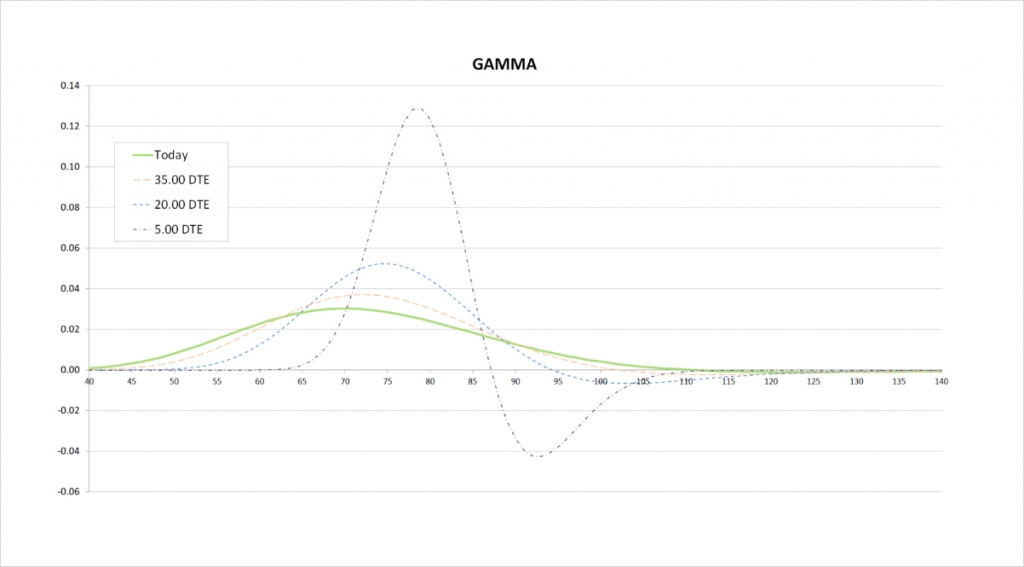
The steeper the delta line, the more extreme the gamma is. The delta line is steepest when the underlying price is around $70, so this is where gamma peaks.
As time passes, we get the hump in the delta close to the short strike that we talked about. This creates two extremes on the gamma chart. One positive peak just below our long strike, and one negative peak close to our short strike. We are long twice as many options at the $80 strike as we are short options at the $90 strike, so the positive peak we see in gamma at the $80 strike is of a greater magnitude.
This gamma is telling us that most of the time our delta increases (or gets less negative) as the underlying price increases. The exception to this is when the underlying price is just above our short strike of $90, where our delta can decrease if the underlying price increases. This effect gets stronger the closer we get to expiry.
Vega
We are short one put, but long another with double the size, so we are net long one put. This means on the whole we gain from an increase in implied volatility, and so have a positive vega.
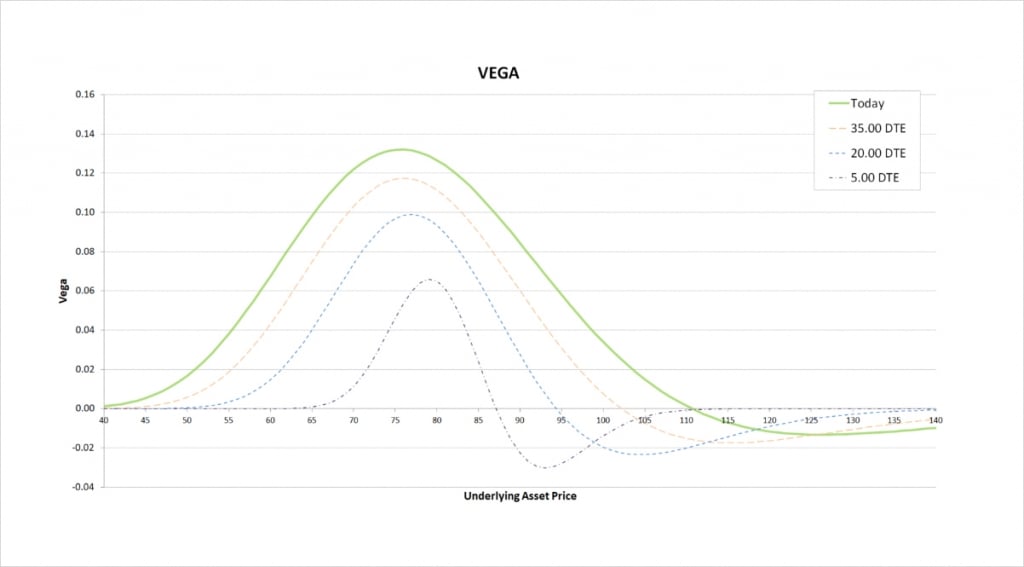
As with the delta and gamma, our vega position looks similar to that of a long put option at first. An increase in implied volatility will increase the value of our short put (which is bad for us), but will also increase the value of our 2 long puts, which more than makes up for it. As time passes though, we have negative vega when the underlying price is above our short strike of $90.
As a reminder, as with everything we’re covering here, if we were instead holding the front spread instead of the back spread, all of these values would be flipped around the x axis. So the front spread will have mostly negative vega, meaning it usually benefits when implied volatility decreases instead.
Theta
We are net long options, so time is against us. Our theta is mostly negative with the put back spread.
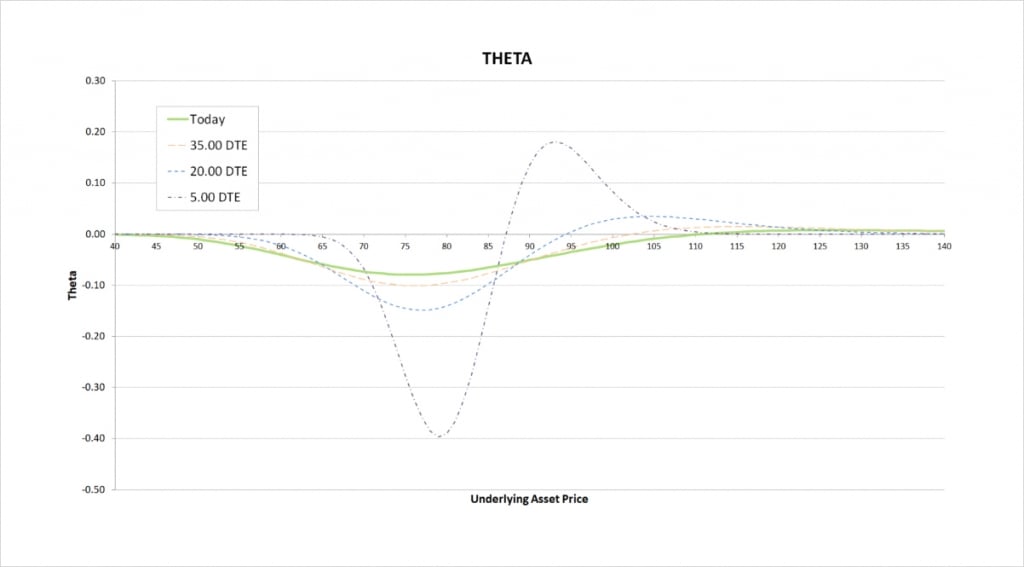
As time passes the negative theta becomes larger in magnitude when we are close to our long strike of $80. We don’t want to be sitting in the belly of the spread as we get closer to expiry. When the options expire, this is where we would suffer the largest loss, and as we get close to expiry this is where we will bleed time value the fastest.
If the price is resting close to our long strike for too long, we may wish to close the back spread early to avoid the increasing pace of losses while price sits there.
As you can tell from all of the Greeks we’ve looked at in the last two lectures, the Greeks for front and back spreads with both puts and calls, are initially similar to those of a single long or short option. As time passes they begin to behave differently depending on where the underlying price is relative to the strikes.
Inverse option contracts
The put back spread looks very similar when using inverse contracts as well.
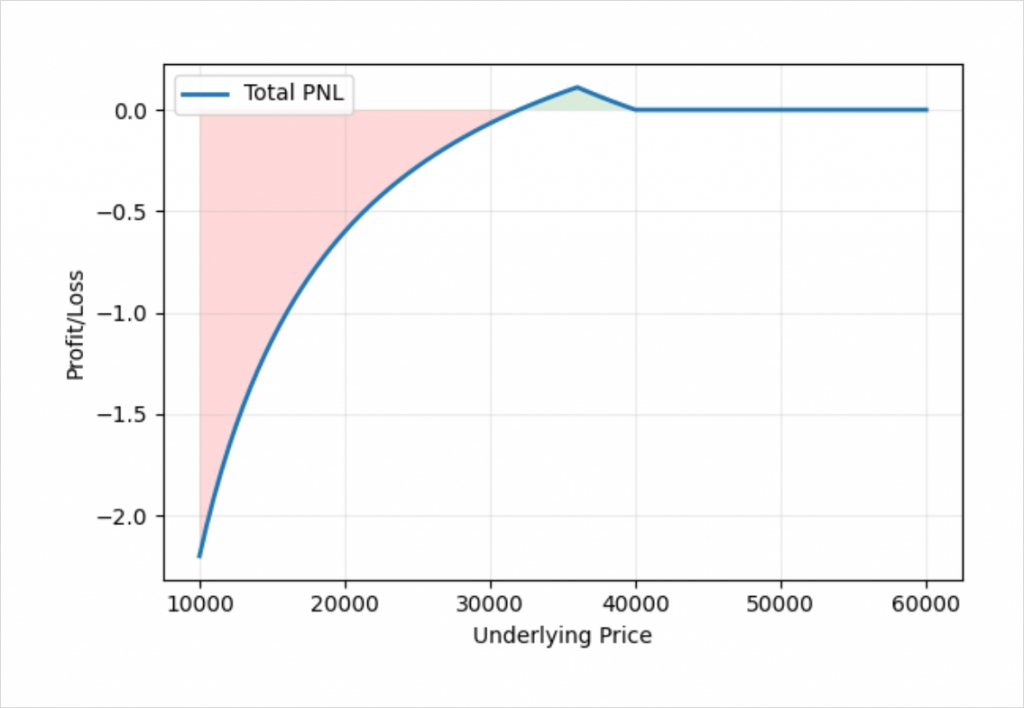
This chart shows the bitcoin payoff at expiry of a put back spread using the bitcoin options on Deribit. In this example we’ve sold one put option with a strike price of $40,000, and purchased two put options with a strike price of $36,000. We collect 0.1 BTC for the $40,000 call, and pay 0.05 each for the $36,000 puts, and therefore establish the position for zero credit or debit.
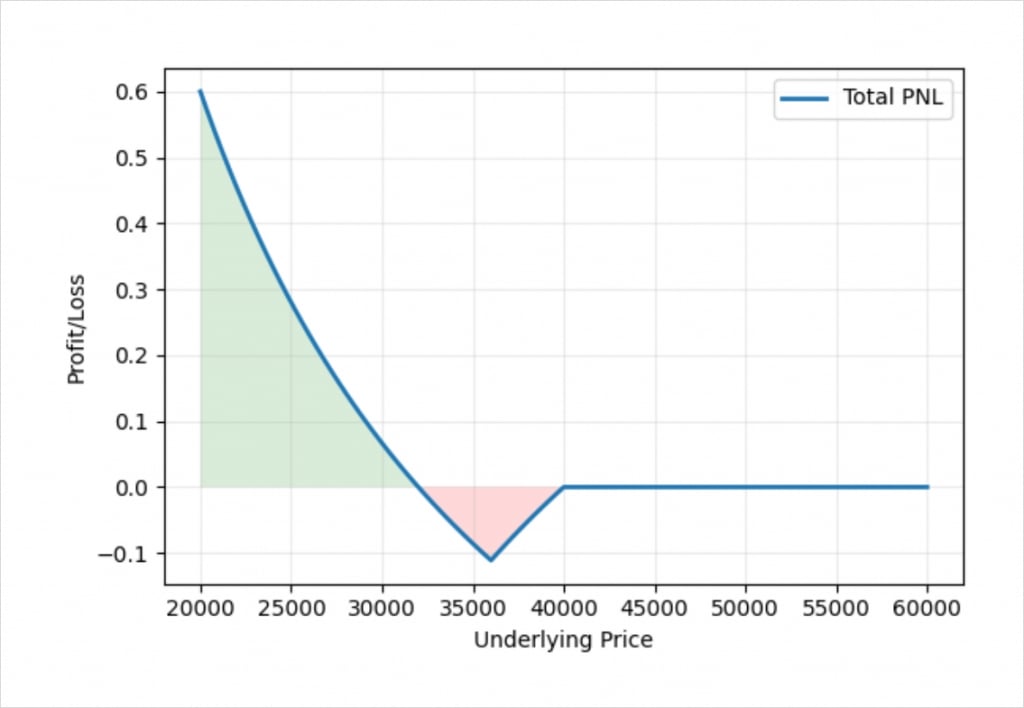
The shape of the profit/loss in bitcoin terms is similar to the profit/loss in dollar terms that we saw earlier, but with the usual curve to the lines we see with inverse contracts. We still have a fixed risk, but much like when we are long a single bitcoin put option, the profit is unlimited.
The rate at which the profit in bitcoin terms increases continues to accelerate as the price of bitcoin decreases further. We can see this even more clearly if we extend the lower boundary of the x axis.
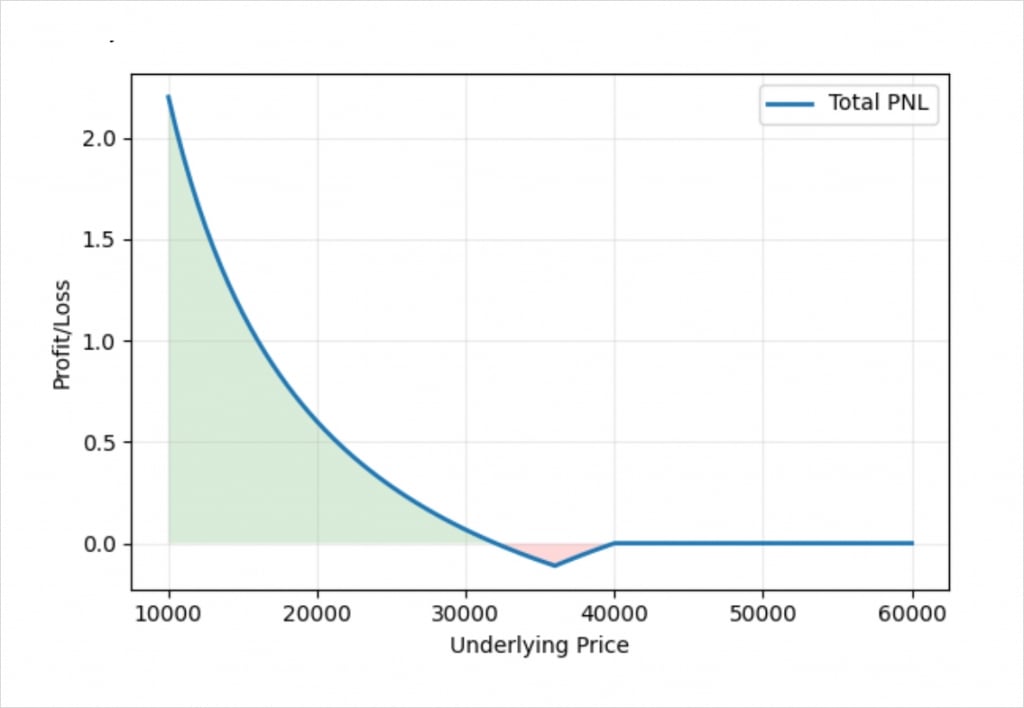
The dollar payout remains linear, and as a net buyer of put options here, this ever increasing amount of bitcoin that it takes to pay us each successive $1 of profit is not a worry to us.
For the trader on the other side of the trade though, the trader with the front spread who is net short inverse put options, this may be much more of a concern.
If the underlying price continues to fall they will likely need to provide more capital to support their position, hedge their exposure, or close the position.
When are back spreads and front spreads attractive?
Put back spreads will be most attractive when we are extremely bearish on an asset that has the potential to make large moves in price. If we are completely wrong on the direction, we will not lose much if anything, but when we are correct and the price decreases significantly, we can make large profits.
We will most easily be able to establish the put back spread for free or even for a net credit, when the IV for OTM puts is similar or lower than the IV for ATM puts.
Conversely, put front spreads will be most attractive when we are most confident that there will not be a large decrease in the underlying price. For put front spreads, ideally we would like the IV for OTM puts to be much higher than the IV for ATM puts. This way we can purchase a single ATM put for relatively cheap, while collecting inflated premiums for the 2 OTM puts that we sell. This will make it easier for us to collect a net credit while establishing the position.

