In this lecture we will work through some examples of how to calculate the profit or loss of a put option position in dollars. For simplicity, for all of these examples, we will ignore any trading fees. Of course in practice to complete the calculation you would subtract whatever fees you have paid as well.
Profit/loss when closing a call option trade early
When an option position is not held to expiry, but closed early, the profit and loss calculation is very simple. Every trade involves a buy order and a sell order, so you simply subtract what you bought the option for from what you sold it for.
If you are long an option, closing the position would be done by selling the option back to another trader, reducing your net position to zero.
If you are short an option, closing the position would be done by buying back the option from another trader, reducing your net position to zero.
In both instances your profit is calculated by subtracting what you bought the option for from what you sold it for.
Example 1:
Let’s use a live price on Tastyworks for the example. Here we have the option chain for SLV, which is a silver ETF (exchange traded fund). The precise instrument we’re looking at here doesn’t matter too much for our profit/loss example, except to say that the contract multiplier for SLV is 100. That is, every 1 option contract represents 100 shares of SLV.
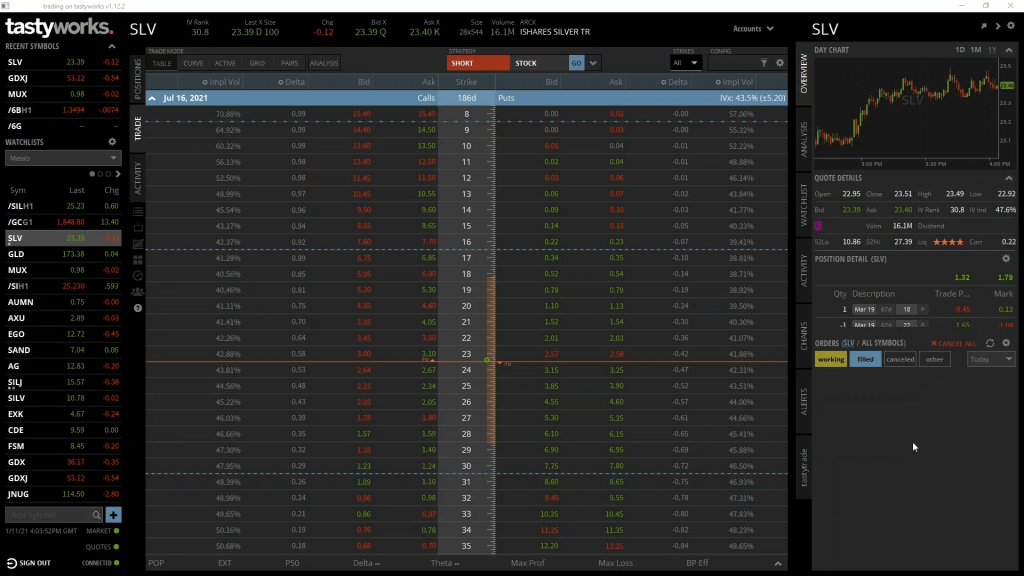
As usual we have strike prices down the centre column, with calls on the left, and puts on the right. We’re only interested in puts for today so we’ll only be looking at the right side of the option chain. Let’s use the put option which has a strike price of $21. The ask price, which is the price we can currently buy it for, is $1.54.
So, let’s assume we buy this put option for $1.54 today. How much profit will we make if the price of SLV moves down in the next few days, and as a result the price of this put option increases to say $4? Remember a put option is the right to sell an asset, so when the price of the asset decreases, all other things being equal, the value of put options for that asset will increase.
We’ve purchased this SLV $21 put option for $1.54, and a few days later it has increased in value to $4. We then decide to close the position before expiration by selling it for $4.
The total profit would then be:
$4 – $1.54 = $2.46
Remember though that the contract multiplier for SLV is 100. This calculation of $2.46 profit is per share. As the contract multiplier is 100, the total then is
$2.46 * 100 = $246.
When we say we bought the put for $1.54, that is per share. For 1 option contract, which represents 100 shares, that brings the total purchase price to $154. Similarly when we sell the contract for a price of $4, that is $4 per share. For 100 shares that is $400.
It’s relatively simple to see that if we bought something for $154, and then sold it for $400, we made a profit of $246. Which is calculated as $400 minus $154.
As we’ve closed the position early, all that matters is the price of our opening and closing orders. The price of SLV at expiry is no longer important to us as our position is now closed.
This is true for all option positions that you completely close early. Your profit is calculated as the price you sold the option for minus the price you bought the option for.
Options held to expiry
At expiration, all of the extrinsic value of an option resulting from volatility and time is gone. To calculate the value of an option when held to expiry we just need to know the strike price and the delivery price at expiration. This gives us the value of the option at expiration, then we simply adjust for the premium paid.
Let’s use the same $21 put option on SLV from example 1, but now we will assume we hold it until it expires.
When a put option has some value at expiration, i.e. when the underlying price at expiration is lower than the strike price, we can calculate the profit/loss of the option position at expiration using this formula:
(Strike Price – Price At Expiration – Premium Paid) * Contract Multiplier * Number Of Contracts
We can plot this formula for different values of ‘Price At Expiration’, which gives us this profit/loss payoff chart.
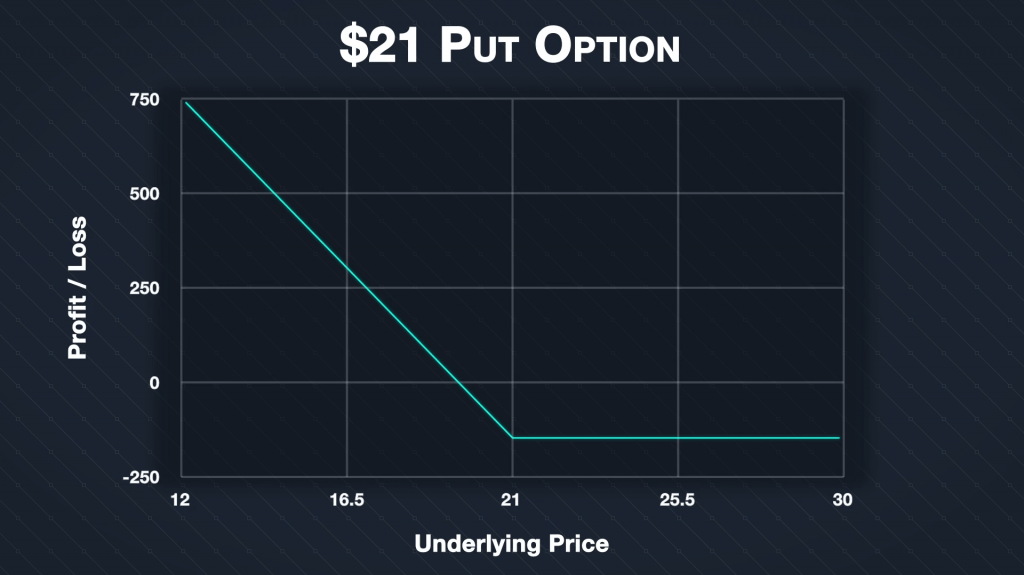
As you can see, for this put option at expiration, the risk is fixed to $1.54 if the price of SLV is anywhere above $21. The profit then increases continuously for any SLV price below $21. Let’s look at some specific examples.
Example 2:
So, this time we’ve purchased the $21 SLV put option for $1.54. Let’s assume that the price of SLV at expiration is $15.
This means we have:
-A price at expiration of $15
-A strike price of $21
-A premium paid of $1.54
-A contract multiplier of 100, and
-A number of contracts of 1
Substituting all these values into the formula, we get:
(21 – 15 – 1.54) * 100 * 1
=4.46 * 100 = $446
That’s $4.46 per share, multiplied by 100 shares. This long put option position has therefore made a profit of $446.
Example 3:
Using the same option still, what if the price at expiration was $20 instead.
We would then have:
-A price at expiration of $20
-A strike price of $21
-A premium paid of $1.54
-A contract multiplier of 100, and
-A number of contracts of 1
Substituting all these values into the formula, we get:
(21 – 20 – 1.54) * 100 * 1
= -0.54 * 100 = -$54
That’s negative $0.54 per share, meaning this long put option position has made a loss of $54. Notice how the price at expiration of $20 is below the strike price of $21. This means the put option did have some value at expiration, $1 per share. However, because we paid $1.54 per share for the option, the value at expiration was not enough to make up for the premium paid, leading to a small loss.
Example 4:
Sticking with the same option, let’s finally see what happens if the price moves in completely the wrong direction, and assume the price at expiration is $30.
We would then have:
-A price at expiration of $30
-A strike price of $21
-A premium paid of $1.54
-A contract multiplier of 100, and
-A number of contracts of 1
This time though, we don’t need to use the formula because the put option has no value at expiry. This is because the price at expiration is above the strike price.
The loss is simply what was paid for the option, which is:
Premium Paid * Contract Multiplier * Number Of Contracts
1.54 * 100 * 1 = $154
Even though the price of SLV increased way above the strike price $21, the loss of the long put option position is limited to the price paid for the option. Even if the price of SLV had increased even further, to say $100, the loss would still only have been the same $154. We’ve mentioned it previously but it’s worth repeating, this fixed risk is one of the most attractive features of buying options.
In summary
Buying a put option has a fixed risk. The maximum loss is limited to the premium paid for the put option. This maximum loss will occur when the option is held to expiration, and the underlying price fails to fall below the strike price by this time.
When closed early, the profit/loss of a long put option is equal to the price it was sold for minus the price paid for the option.
When the call option is held to expiry, and the underlying price is less than the strike price, we can use this formula to calculate the profit/loss precisely:
(Strike Price – Price At Expiration – Premium Paid) * Contract Multiplier * Number Of Contracts
The further below the strike price the underlying price has moved, the more profit a long put option will make.

