We mentioned in the previous lecture that the theta of an option is not static. One variable that has a major influence on theta is the underlying asset price, and where it currently is relative to the strike price of each option.
Let’s take a look at multiple options that share the same underlying asset price, days to expiry, and implied volatility. The only difference between these options is of course the strike price, and therefore where they sit relative to the underlying asset price.
This chart shows the theta for all options of a fictional asset with a current price of $100, 30 days to expiry, and implied volatility (IV) of 40%. The strikes range from $50 to $150.
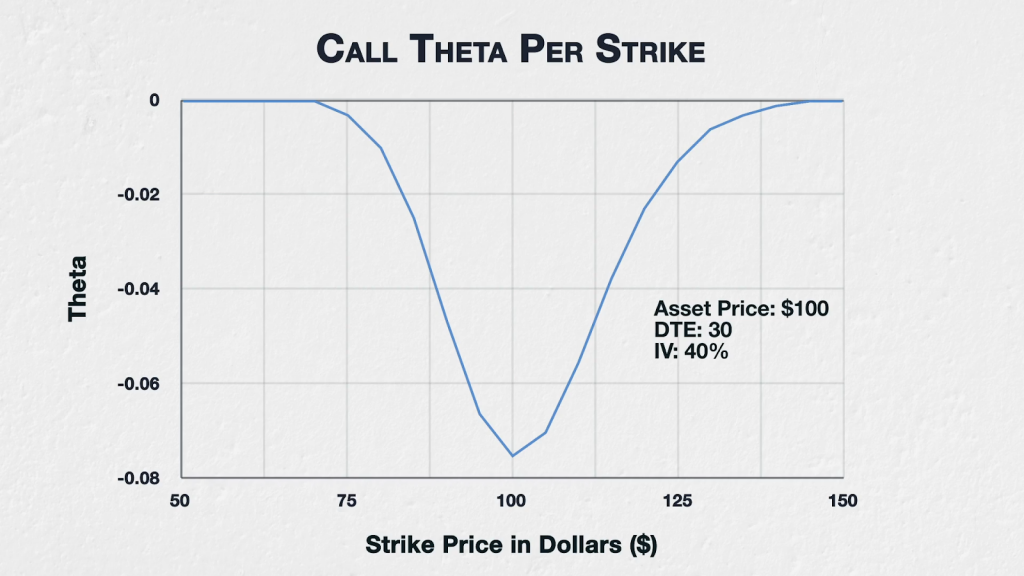
I’ve chosen to only show the call values here, because with interest and dividend rates both set to zero, the theta will be equal for the put and call at each strike price. It’s worth also mentioning briefly that interest rates and dividends can shift the curve of theta for puts and calls, however as both are assumed to be zero on deribit, we will not spend time covering this in any detail. If you wish to model this effect yourself, this black scholes script for excel will allow you to do this with ease. You can find the script here:
https://www.philadelphia-reflections.com/blog/2394.htm
The underlying price here is $100, and as you can see, this is where theta is greatest. This means the ATM call option with a strike price of $100, will lose more value over the next 24 hours than for example the ITM $90 call or the OTM $110 call.
If we move further away from the current underlying price, this trend continues, with the $80 call having smaller theta than the $90 call, and the $120 call having smaller theta than the $110 call.
More generally, theta is greatest for ATM options, and then reduces the further away from the current underlying price the strike price is. This stands to reason because extrinsic value is greatest for ATM options, so they have the most value to lose. Theta is an erosion of extrinsic value by the passage of time, and at expiration all extrinsic value must be gone. So, assuming options with the same expiry date, the options with more extrinsic value to lose (ATM options), will lose more dollars over a given time period than options with less extrinsic value to lose (ITM and OTM options).
Notice that we are specifically talking about extrinsic value here, not the total option price, which also includes intrinsic value. This is because time has no effect on the intrinsic value of an option, intrinsic value just being a reflection of how far in the money the option is. So an ITM option will have a higher total price than an OTM option, however part of this higher total will come from it’s intrinsic value, which does not erode as time passes. This is why both OTM and ITM options have smaller theta than the ATM option, because they are only losing the extrinsic portion of their value as time passes.
In summary
Where the strike price of an option is in relation to the underlying price, will have an impact on the theta of that option.
ATM options have the most extrinsic value to lose, and so will have the greatest amount of theta. That is, they will lose the most value over the next 24 hours, assuming all else remains stable.
As we move away from the current underlying price in either direction, both ITM and OTM options will have smaller theta than the ATM options of the same expiry.


