Implied volatility will also affect the theta of options. Let’s look at the call options from the example in the previous lecture, and see how the theta of these options would be affected by different levels of implied volatility.
This chart shows the theta for all options of a fictional asset with a current price of $100, 30 days to expiry, and varying levels of implied volatility (IV). The strikes range from $50 to $150.
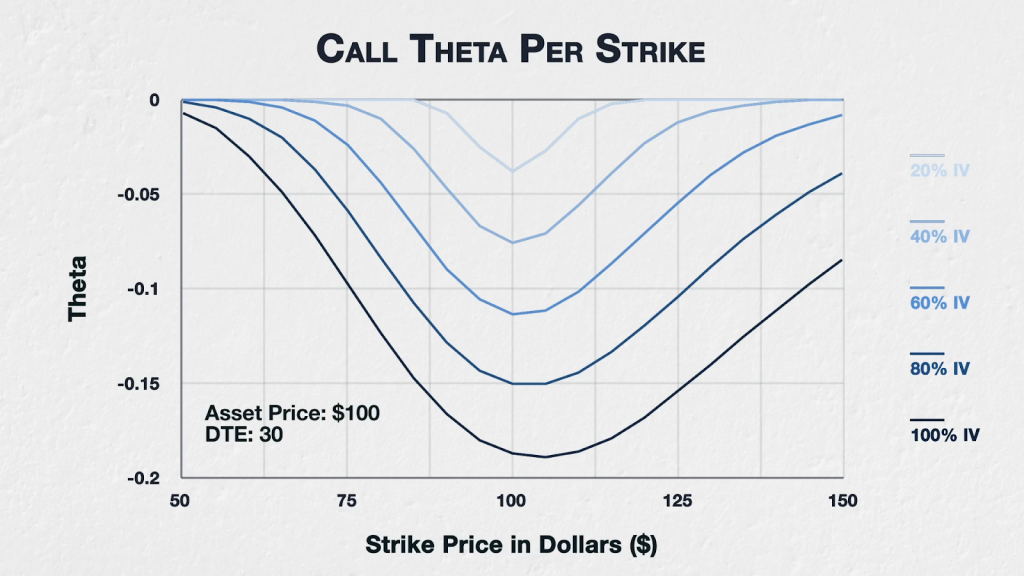
This is essentially the same chart we looked at in the previous lecture, except instead of only looking at the 40% IV level, we have included a separate line for five different IV levels from 20% up to 100%.
The 40% line is exactly the same as in the last lecture, and for each of the other four lines, the only parameter that has been changed is the value for implied volatility.
As you can see, as IV increases, the theta of all call options increases. The basic characteristic of the most theta being concentrated around the ATM strikes, and then decreasing in both directions, still holds as IV increases. Though as you may have noticed, and well done if you did, that when we get to much higher IV (at 80% and 100%) the peak (or actually trough here) is pushed a little higher in price than the ATM strike, and the line is a little less symmetrical around the peak, being skewed to the upside.
Remember that IV is essentially just a way of writing the option prices in the form of an annualised volatility. This allows for much easier analysis and comparison. Assuming all other parameters remain the same, as they do here, higher IV means higher option prices. Which in turn means they have more value to lose in the same amount of time, therefore the theta (or time decay) is also higher.
In summary
An increase in IV, means an increase in option prices. The options then have more value to lose in the same amount of time, and therefore their theta is higher. This is true for all options, whether they are in, at, or out of the money.
The options close to the current underlying price will have the most extrinsic value to lose and therefore the most theta. This decreases in both directions away from the current underlying price.
When IV is very high, this can increase the strike price at which theta is greatest such that it is higher than the current underlying price, but the general principle remains; assuming all else remains the same, higher IV means higher theta, and lower IV means lower theta.


